Двойственный симплекс-метод и доказательство теоремы двойственности
Страница 2
(1.3) Aj = DXj (j= 1,2, , , n).
Для оптимального плана получаем
(1.4) A0 = DX*,
где X* = (x*1, x*2, …, x*m).
Обозначим через 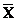 матрицу, составленную из коэффициентов разложения векторов Аj (j = 1, 2, ., n), записанных в табл. 1.1. Тогда, учитывая соотношения (1.3) и (1.4), получаем:
матрицу, составленную из коэффициентов разложения векторов Аj (j = 1, 2, ., n), записанных в табл. 1.1. Тогда, учитывая соотношения (1.3) и (1.4), получаем:
(1.5) A = D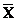 , D-1A =
, D-1A = 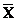 ,
,
(1.6) A0=DX*; D-1A0 = X*,
(1.7) min Z= C*X*,
(1.8) 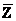 = C*
= C*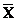 —C £ 0,
—C £ 0,
где С* = (C*1, C*2, …, C*m), С = (C1, C2, …, Cm, Cm+1, …, Cn), a 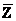 = (C*X1 – C1; С*Х2 - С2, ., C*Xn – Cn) = (Z1 – С1; Z2 - C2; ., Zn — Cn) — вектор, компоненты которого неположительны, так как они совпадают с Zj — Cj £ 0, соответствующими оптимальному плану.
= (C*X1 – C1; С*Х2 - С2, ., C*Xn – Cn) = (Z1 – С1; Z2 - C2; ., Zn — Cn) — вектор, компоненты которого неположительны, так как они совпадают с Zj — Cj £ 0, соответствующими оптимальному плану.
Оптимальный план исходной задачи имеет вид X* = D-1 А0, поэтому оптимальный план двойственной задачи ищем в виде
(1.9) Y* = C*D-1.
Покажем, что Y* действительно план двойственной задачи. Для этого ограничения (1.2) запишем в виде неравенства YA — С £ 0, в левую часть которого подставим Y*. Тогда на основании (1.9), (1.5) и (1.8) получим
Y* А – С = С* D-1А – С = С* 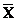 - С £ 0,
- С £ 0,
откуда находим Y*A £ С.
Так как Y* удовлетворяет ограничениям (1.2), то это и есть план двойственной задачи. При этом плане значение линейной функции двойственной задачи f (Y*) = Y*A0. Учитывая соотношения (1.9), (1.6) и (1.7), имеем
(1.10) f (Y*) = Y*A0 = C*D-1 A0 = C*X* = min Z(X).
Таким образом, значение линейной функции двойственной задачи от Y* численно равно минимальному значению линейной функции исходной задачи.
Докажем теперь, что Y* является оптимальным планом. Умножим (1.1) на любой план Y двойственной задачи, а (1.2) — на любой план X исходной задачи: YAX=YA0=f (Y), YAX £ СХ = Z (X), отсюда следует, что для любых планов Х и Y выполняется неравенство
(1.11) f (Y) £ Z (X).
Этим же соотношением связаны и экстремальные значения max f (Y) £ min Z (Х). Из последнего неравенства заключаем, что максимальное значение линейной функции достигается только в случае, если max f (Y) = min Z (X), но это значение [см. (1.10)] f (Y) достигает при плане Y*, следовательно, план Y* — оптимальный план двойственной задачи.
Аналогично можно доказать, что если двойственная задача имеет решение, то исходная также обладает решением и имеет место соотношение max f (Y) = min Z (X).
Для доказательства второй части теоремы допустим, что линейная функция исходной задачи не ограничена снизу. Тогда из (1.11) следует, что f (Y) £ -¥ . Это выражение лишено смысла, следовательно, двойственная задача не имеет решений.
Аналогично предположим, что линейная функция двойственной задачи не ограничена сверху. Тогда из (1.11) получаем, что Z (X) ³ +¥. Это выражение также лишено смысла, поэтому исходная задача не имеет решений.
Доказанная теорема позволяет при решении одной из двойственных задач находить оптимальный план другой.
Исходная задача. Найти минимальное значение линейной функции Z = x2 – x4 – 3x5 при ограничениях
 x1 + 2x2 - x4 + x5 = 1,
x1 + 2x2 - x4 + x5 = 1,
- 4x2 + x3 + 2x4 – x5 = 2, xij ³ 0 (j = 1, 2, …, 6)
3x2 + x5 + x6 = 5,
Здесь матрица-строка С = (0;. 1; 0; —1; — 3, 0), матрица-столбец

 1 1 2 0 -1 1 0
1 1 2 0 -1 1 0
A0 = 2 A = 0 -4 1 2 -1 0
3 0 3 0 0 1 1
 1 0 0
1 0 0
2 -4 3
A’’ = 0 1 0
-1 2 0
1 -1 0
0 0 1
Двойственная задача. Найти максимальное значение линейной функции f = y1 + 2y2 +5y3 при ограничениях
 y1 £ 0,
y1 £ 0,
2y1 – 4y2 + 3y3 £ 1,
y2 £ 0,
-y1 + 2y2 £ -1,
y1 – y2 + y3 £ -3,
y3 £ 0.
Решение исходной задачи находим симплексным методом (табл. 1.2).
|
i |
Базис |
С базиса |
A0 |
0 |
1 |
0 |
-1 |
-3 |
0 |
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
1
2
3 |
A1
A3
A6 |
0
0
0 |
1
2
5 |
1
0
0 |
2
-4
3 |
0
1
0 |
-1
2
0 |
1
-1
1 |
0
0
1 |
|
m + 1 |
Zi - Cj |
0 |
0 |
-1 |
0 |
1 |
3 |
0 |
|
1
2
3 |
A5
A3
A6 |
-3
0
0 |
1
3
4 |
1
1
-1 |
2
-2
1 |
0
1
0 |
-1
1
1 |
1
0
0 |
0
0
1 |
|
m + 1 |
Zi - Cj |
-3 |
-3 |
-7 |
0 |
4 |
0 |
0 |
|
1
2
3 |
A5
A4
A6 |
-3
-1
0 |
4
3
1 |
2
1
-2 |
0
-2
3 |
1
1
-1 |
0
1
0 |
1
0
0 |
0
0
1 |
|
m + 1 |
Zi - Cj |
-15 |
-7 |
1 |
-4 |
0 |
0 |
0 |
|
1
2
3 |
A5
A4
A2 |
-3
-1
1 |
4
11/3
1/3 |
3
-1/3
-2/3 |
0
0
1 |
1
1/3
-1/3 |
0
1
0 |
1
0
0 |
0
2/3
1/3 |
|
m + 1 |
Zi - Cj |
-46/3 |
-19/3 |
0 |
-11/3 |
0 |
0 |
-1/3 |