Обучение построению дедуктивных умозаключений при решении задач в 4 классе
Страница 6
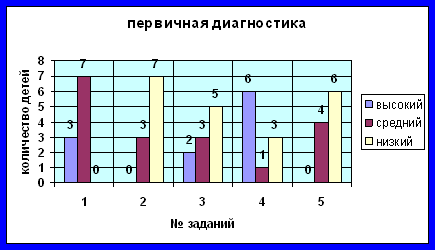
1. Констатирующий этап позволяет нам выявить уровень развития логического мышления у учащихся, выявить показатели сформированности умений, таких как: умения решать нестандартные задачи и выстраивать логические цепочки. Определить приемы активизации творческой мыслительной деятельности с помощью дедуктивных умозаключений на уроках математики у учащихся 4-х классов. Полученные с помощью констатирующего эксперимента данные помогут определить задачи и разработать содержание и методы формирующего этапа исследования:
1. Подготовленные нами варианты работ раздаются учащимся. Работа выполняется в двух аналогичных вариантах (варианты работ см. приложение 4).
2. Учителем дается инструкция к выполнению каждого задания, указывая на то, что последующее будут сложнее предыдущего.
3. Итог: в полученных работах можно выделить 3 уровня (критерии оценивания):
Ø Высокий(5 заданий)
Ø Средний(3-4 задания)
Ø Низкий(меньше 3 заданий)
2. Формирующий этап.
На формирующем этапе своей работы мы ставим следующие задачи:
1. Развивать логическое мышление.
2. Формировать умение строить дедуктивные умозаключения и пользоваться ими на практике.
3. Развивать мыслительные операции (анализ, синтез, сравнение, сопоставление).
Содержание работы.
Ø давать задания с учетом возможностей детей, постепенно усложняя;
Ø перед началом работы детей над тем или иным заданием, давать четкую инструкцию по его выполнению;
Ø контролировать выполнение детьми данных заданий;
Ø осуществлять контроль уровня сформированности умения строить дедуктивные умозаключения.
На данном этапе, на практике реализуется составленная группа заданий, которые способствуют развитию логического мышления, путем построения дедуктивных умозаключений.
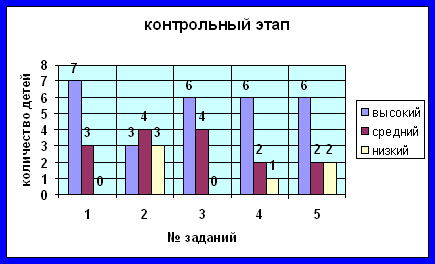
3. Контрольный этап.
На данном этапе эксперимента с классом проводились такие формы работ:
Ø Открытые уроки (содержание уроков см. приложение 5)
Ø Практическая работа с классом (математический диктант).
Ø Практическая работа с классом (см. приложение 3)
Цель: Проверить уровень сформированности умения строить дедуктивные умозаключения у учащихся при решении математических задач.
Математический диктант.
Данный вид работы позволяет учителю быстро и точно определить пробелы в знаниях учащихся. Мы предлагаем математический диктант, который применялся на преддипломной практике.
1
Начни или закончи высказывание:
1. Чтобы узнать, на сколько одно число больше или меньше, чем другое, надо…
2. При умножении единицы на любое число получается…
3. … нуля на любое число получается нуль.
4. Для того чтобы найти скорость, нужно…
5. Для того чтобы найти значение периметра прямоугольника, нужно…
6. … , то значение разности равно нулю.
7. … прибавить вычитаемое, то получится уменьшаемое.
2
1. У Вити и Мити было одинаковое количество гвоздей. Витя отдал Мите 3 гвоздя. Насколько больше гвоздей стало у Мити, чем у Вити?
2. «Вот вам три таблетки, – сказал доктор. – Принимайте по одной через каждые 2 часа». Через сколько времени будет принята последняя таблетка?
3. Петров на 8 лет моложе, чем Светлов. Петров на 3 года старше, чем Денисов. Кто моложе всех? На сколько лет Светлов старше Денисова?
3
Вставь такие числа, чтобы неравенства были верными:
х 6 > х 9
Таким образом, целью данного диктанта является закрепление таких навыков как сравнение значения выражения с числом, нахождение определенной закономерности, умение использовать дедуктивные умозаключения при вычислениях и нахождении логических цепочек.
Проводилось множество диктантов, в течение нашей работы, направленных на закрепление и другого материала, такого как: уравнения, порядок действий. Данный вид работы мы реализовывали, не выходя за рамки курса изучения математики. Работы такого рода служили пропедевтикой по изучаемой нами теме и помогали при достижении поставленных нами целей.
3.1. Итог: проверив работы учащихся, мы сделали вывод о том, что у учащихся формируется навык использования дедуктивных умозаключений при различных видах работ, таких как: составление выражений по условию задачи, навык сравнения выражения с числом, построение логических цепочек. Большинство учащихся допустили ошибки в задании, связанном с расстановкой знаков действий, что говорит о том, что надо как можно больше работать над вариативностью мышления, чтобы научить детей смотреть и видеть на несколько шагов вперед. В приложении 1 и 2 приведены варианты заданий, которые способствовали реализации нашего исследования и приближению нашей цели к реальности.
На диаграмме контрольного этапа мы видим, что динамика развития исследуемой проблемы весьма заметна. Если при первичной диагностики с теоретическим материалом справилось 30% учащихся, то после проведенной нами работы этот показатель повысился до 70%, что говорит о правильно подобранных методах и формах работы с детьми. Но, решая нестандартные задачи, учащиеся все еще могут ошибаться и для того, чтобы избежать дальнейших ошибок, нужно постоянно поддерживать интерес детей и развивать их способности.
3.2.Вывод: Констатирующий эксперимент подтвердил положения, выдвинутые в теоретической части данной работы. Большинству учащихся трудно выделять определенные закономерности, выстраивать логические цепочки и решать нестандартные задачи. Поэтому на формирующем этапе нашей работы мы определили группу заданий, решение которых способствовало развитию умения строить дедуктивные умозаключения.
Группа заданий и форма выполнения, предложенных на формирующем этапе (см. приложение 3), вызвали интерес у учащихся. Нужно отметить активность и сознательность учащихся при их выполнении. На наш взгляд, такой активизации способствовали занимательность и наглядность заданий.
При выполнении первых заданий у детей возникли трудности в построении логических цепочек, опираясь на дедуктивные рассуждения. Но в дальнейшем дети стали допускать меньше ошибок при ответах на вопросы и выполнении практических заданий.
Заключение.
Основной целью математического образования должно быть развитие умения математически, а значит, логически и осознанно исследовать явления реального мира. Реализации этой цели может и должно способствовать умения строить дедуктивные умозаключения при решении на уроках математики различного рода математических задач.
Итак, в своей работе мы исследовали и доказали необходимость использования дедуктивных умозаключений при решении задач. Именно разработав группу заданий, мы сможем улучшить математическую подготовку учащихся, реализуя на практики поставленную нами цель. Организация различных форм работы с задачами поможет нам развивать у детей логическое мышление, с помощью умения строить дедуктивные умозаключения, и математические способности. А так же поможет нам расширить детский кругозор и разрушить стереотипы у детей при решении различного рода задач. Исходя из выше сказанного, мы можем заключить, что действительно, развивать умение строить дедуктивные умозаключения, учить рассуждать и доказывать на уроках математики, возможно при условии использования на уроках системы всевозможных задач, проводя из урока в урок аналитико-синтетическую работу с каждым из заданий. И как мы говорили ранее, систематическое использование на уроках математики и внеурочных занятиях специальных задач и заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
В данной работе мы исследовали вопрос возникновения и развития теории дедукции, изучили основные понятия. Рассмотрели психолого-педагогические особенности младших школьников, место и роль дедуктивных умозаключений при решении математических задач. А так же показали пропедевтические задания, которые можно использовать при обучении учащихся строить правильные дедуктивные умозаключения.