Дискретная математика (Конспекты 15 лекций)
Страница 8
Планарные графы.
Определение.
Укладкой графа называется такое его геометрическое изображение, при котором ребра пересекаются только в вершинах. Если существует укладка графа на плоскости, то граф называется планарным.
Сама же укладка графа без пересечения ребер называется плоским графом.
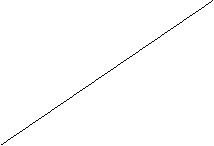Любой граф можно изобразить в трехмерном пространстве без пересечения ребер.
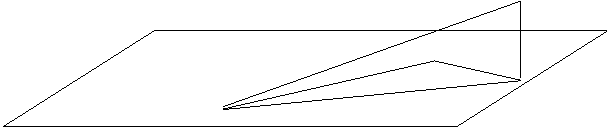
Для любого графа xi, соединяющего 2 вершины проводим новую плоскость, содержащую эту прямую, а ребро рисуем на плоскости.
Граф будет планарным, если существует его укладка на сфере.
Доказательство следует из взаимно однозначного соответствия точек на сфере с точками плоскости из стереографических проекций.
Следствие. Граф любого выпуклого многогранника планарен.
Ребра плоского графа разбивают плоскость на несколько частей, одна из которых бесконечна. Эти части и являются гранями плоского графа.
Теорема Эйлера о плоских графах.
Формула Эйлера.
Для плоского графа справедливо соотношение.
M – N + P = 2.
Докажем индукцией по числу граней
P = 1
Если P = 1, то граф – дерево. В нем нет ни одного цикла. У дерева число вершин больше числа ребер на 1.
M = N + 1
N + 1 – N + 1 = 2 – справедливо.
Пусть p = k, и утверждение верно.
Тогда оно верно и при P= k+1
Берем ребро графа, отделяющее бесконечную грань от внутренних и удаляем это ребро из графа. Т.к. оно циклическое, то в новом графе g1 (он также будет связным) число вершин M останется прежним.
N1 = N – 1
P1 = P – 1
M = M
k + 1-1 = k
Для g1 справедливо предположение индукции.
M1 + N1 + P1 = 2
M – N – 1 + K = 2
M – N + K – 1 = 2
M – N + P = 2
Что и требовалось доказать.
Следствие 1.
Для плоского связного простого графа справедливо соотношение
n <= 3*(m-2)
Следствие 2.
Для плоского связного простого графа без треугольных граней справедливо соотношение
n <= 2*(m-2)
Следствие 3.
Граф K5 – непланарен.
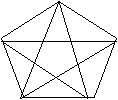m > 2
И если бы он был плоским, то для него было бы справедливо следствие 1.
N <= 3*(m-2)
10 <= 9 – неверно.
Противоречие. Значит, он не может быть нарисован плоским.
Следствие 4.
Граф K3-3 непланарен.
Нет треугольных граней.
Если бы он был плоским, то для него было бы справедливо следствие 2.
9 <= 2*(6-2)
9 <= 8 – неверно.
Противоречие из предположения, что он не может быть плоским.
Операцией разбиения ребра графа называется следующая процедура:
Ребро удаляется из графа, и в граф добавляется новая вершина, соединенная новыми ребрами с концами данного ребра.
Два графа называются гомеоморфными, если каждый из них может быть получен из одного и того же графа путем применения конечного числа раз операции разбиения ребер.
Теорема Понтрягина – Куратовского.
Чтобы граф был планарным, необходимо и достаточно, чтобы он не содержал гомеоморфных подграфов.
Лекция 13
Сети. Пути в орграфах. Остовы минимальной длины
Определение. Двуполюсной сетью называется связный граф без петель с двумя выделенными вершинами, которые называются полюсами.
Двуполюсная сеть называется сильно связанной (связной), если через любое ребро проходит простая цепь, соединяющая полюса. В ней нет повторяющихся вершин.
Параллельная сеть – сеть вида
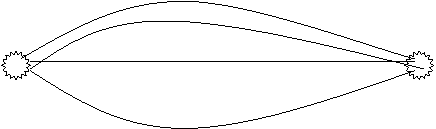Последовательная сеть – сеть вида
П (пи) сети – последовательно-параллельные сети
Примеры П-сетей
Такая сеть называется мостиковой.
Контактными схемами называются сильносвязные двуполюсные сети, каждому ребру которой поставлено в соответствие x или NOT(x).
X Not Y
Z Not X
Любой контактной схеме (КС) можно поставить в соответствие булеву функцию (функцию проводимости) по правилу:
Для любой простой цепи, соединяющей полюса, записываем ЭК тех переменных, которыми помечены ребра этой цепи.
Затем берем дизъюнкцию всех ЭК. Получим искомую функцию проводимости.
Если в контактной схеме будут стоять переключатели (релейные контакты), которые будем считать замкнутыми, если выражение, стоящее у ребра равно 1 или в противном случае разомкнутыми, то при подаче на полюса разности потенциалов (электрического тока) контактная схема будет проводить ток при таких и только при таких состояниях контактов, при которых значение функции равно 1.
Минимальной контактной схемой для функции называется контактная схема, для которой эта функция является функцией проводимости. Эта схема содержит наименьшее число ребер.
Чтобы построить минимальную КС, надо выписать минимальную ДНФ для данной функции, упростить путем вынесения за скобки, нарисовать П-сеть, реализующую КС для функции и постараться найти мостиковые соединения.
Минимальные пути в графах
Путем в графе (в орграфе) называется маршрут, движение по которому любого ребра проходит в соответствии с направлением этого ребра.
Контуром в орграфе называется замкнутый путь, в котором вершины не повторяются (кроме первой и последней).
Орграф, в котором нет ни одного контура, называется бесконтурным.
Первая задача о минимальном пути.
Дан граф. Выделено две вершины. Найти путь из одной вершины в другую, состоящий из наименьшего числа ребер.
Введем обозначения
Г(V) – множество вершин, в которые можно попасть из вершины V, пройдя только по одному ребру в его направлении.