Аналогии в курсе физики средней школы
Страница 2
Выведем уравнение свободных незатухающих электромагнитных колебаний в контуре и колебаний горизонтального пружинного маятника. Применяя к пружинному маятнику закон сохранения энергии, получим равенство: 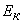 +
+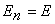 , где
, где
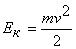 ,
, 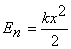 , тогда имеем
, тогда имеем
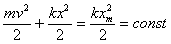 (1)
(1)
Так как
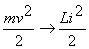 и
и 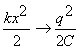 получаем
получаем

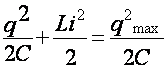 =const (2)
=const (2)
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии. В уравнении (2) i=q' - мгновенное значение силы тока, qmax - максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем вывод о зависимости силы тока от величины заряда и находим значение максимальной силы тока:
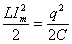 ;
; 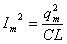 Откуда
Откуда
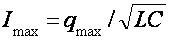 при q=0.
при q=0.
Как видно формально с точки зрения математики уравнения (1) и (2) являются одинаковыми.
Решаем уравнение (2): производная полной энергии по времени равна нулю, так как энергия постоянна.
Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей.
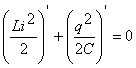 или
или
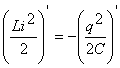 (3)
(3)

Физический смысл уравнения (3) состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля; знак “минус” указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает (и наоборот). Поэтому полная энергия не меняется.
Вычисляя обе производные получаем:
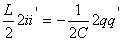
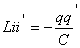
так как 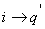 , тогда
, тогда
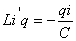 и
и 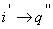
получаем
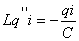
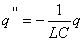 (4)
(4)
Уравнение (4) является основным уравнением, описывающем процессы в колебательном контуре.
Рассмотрим колебания вертикального пружинного и математического маятников.
 Выведем груз из положения равновесия, растянув пружину на длину Хm (рис.2) и отпустим. (Амплитудное растяжение пружины Xm должно быть таково, чтобы был справедлив закон Гука
Выведем груз из положения равновесия, растянув пружину на длину Хm (рис.2) и отпустим. (Амплитудное растяжение пружины Xm должно быть таково, чтобы был справедлив закон Гука 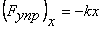 и выводимая на его основе формула потенциальной энергии пружины.)
и выводимая на его основе формула потенциальной энергии пружины.)
 Рис.2
Рис.2

 Мгновенные значения координаты груза х в процессе колебаний лежат в пределах -xm£x£xm . По закону сохраненья энергии имеем:
Мгновенные значения координаты груза х в процессе колебаний лежат в пределах -xm£x£xm . По закону сохраненья энергии имеем:

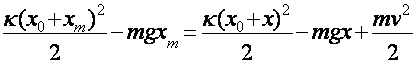 (5)
(5)
где X0=mg/k - статическое растяжение пружины (потенциальную энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза, обозначенного на рис. 2 пунктиром). Учитывая, что 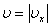 и
и 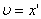 , получим уравнение колебаний
, получим уравнение колебаний
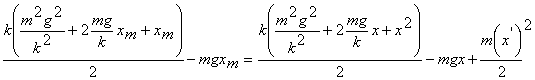
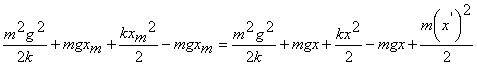

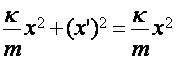 =соnst
=соnst (6)
(6)
Как видно уравнения колебаний горизонтального и вертикального пружинных маятников одинаковы.
Ускорение свободного падения g, имеющееся в уравнении (5), отсутствует в полученном уравнении колебаний. Следовательно, колебания груза на пружине не зависят от g и одинаковы, например, на Земле и Луне.
Хотя в дифференциальные уравнения (1) и (6) входят разные величины, математически они эквивалентны.
По аналогии с уравнением (4) описывающем процессы в колебательном контуре, запишем уравнение колебания пружинного маятника:
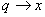 ;
; 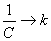 ;
; 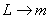
получим
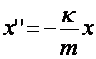 , (7)
, (7)
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия на длину дуги sm<<l и отпустим. Мгновенная высота подъема маятника
рис.3

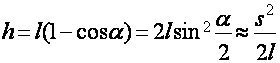
так как при a<<1 можно считать 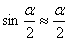 , а s=la. По закону сохранения энергии имеем:
, а s=la. По закону сохранения энергии имеем:
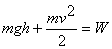 , где
, где 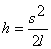
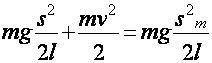
или
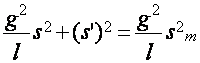 =const (8)
=const (8)
По аналогии с формулами (4) и (7) x®q®s; 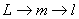 ;
; 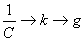 получаем:
получаем:
S``= - 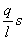 (9)
(9)
Различие уравнений (1), (6) и (9) состоит только в обозначениях и физическом смысле входящих в них величин.
Если не предполагать sm<<l (соответственно am=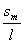 <<1 рад.), то получится сложное уравнение, решить которое в рамках школьного курса невозможно. Оно будет описывать колебания, период которых зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит от am, однако при sm<<l рад. этой зависимостью можно пренебречь.
<<1 рад.), то получится сложное уравнение, решить которое в рамках школьного курса невозможно. Оно будет описывать колебания, период которых зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит от am, однако при sm<<l рад. этой зависимостью можно пренебречь.
Процессы в колебательном контуре станут понятнее учащимся при рассмотрении преобразований энергий, которые происходят при колебаниях, используя таблицу 2.
|
Время |
Колебательный контур |
Пружинный маятник |
|
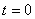
|
На конденсаторе находится заряд q0; энергия электрического поля Wэ максимальна. Энергия магнитного поля Wм равна нулю
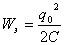 ; ; 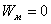
|
Смешение X0 тела от положения равновесия — наибольшее; его потенциальная энергия Wп максимальна, кинетическая Wк равна нулю
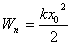 ; ;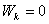
|
|
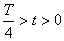
|
При замыкании цепи конденсатор начинает разряжаться через катушку: возникает ток и связанное с ним магнитное поле. Вследствие самоиндукции сила тока нарастает постепенно; энергия электрического поля преобразуется в энергию магнитного поля
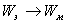
|
Тело приходит в движение, его скорость возрастает постепенно. Потенциальная энергия преобразуется в кинетическую
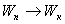
|
|
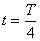
|
Конденсатор разрядился, сила тока I0 максимальна, энергия электрического поля равна нулю, энергия магнитного поля максимальна
Wэ=0; 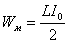
|
При прохождении положения равновесия скорость v0, тела и его кинетическая энергия максимальны, потенциальная энергия равна нулю
Wп=0; 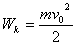
|
|
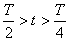
|
Вследствие самоиндукции сила тока уменьшается постепенно; на конденсаторе начинает накапливаться заряд и
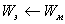
|
Тело, достигнув положения равновесия, продолжает движение по инерции с постепенно уменьшающейся скоростью и
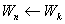
|
|
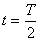
|
Конденсатор перезарядился; сила тока в цепи равна нулю
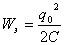 ; Wм=0 ; Wм=0
|
Пружина максимально растянута: скорость тела равна нулю
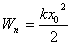 ; Wk=0 ; Wk=0
|
|
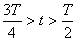
|
Разрядка конденсатора возобновляется; ток течет в противоположном направлении; сила тока постепенно возрастает
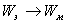
|
Тело начинает движение в противоположном направлении с постепенно увеличивающейся скоростью
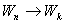
|
|
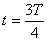
|
Конденсатор полностью разрядился; сила тока I0 в цепи максимальна
Wэ=0; 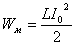
|
Тело проходит положение равновесия, его скорость максимальна
Wп=0; 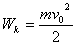
|
|
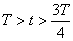
|
Вследствие самоиндукции ток продолжает течь в том же направлении, конденсатор начинает заряжаться 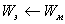 |
По инерции тело движется к крайнему положению
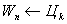
|
|
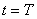
|
Конденсатор снова заряжен, ток в цепи отсутствует, состояние контура аналогично первоначальному
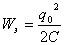 ; Wм=0 ; Wм=0
|
Смещение тела максимально, его скорость равна нулю и состояние аналогично первоначальному
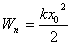 ; Wk=0 ; Wk=0
|