Аналогии в курсе физики средней школы
Страница 3
§ 2. Решение уравнений, описывающих колебания в пружинном и математическом маятниках.
Найдем решение уравнения:
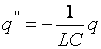 (1)
(1)
Нельзя считать, что  или
или  , так как вместо
, так как вместо 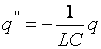 получилось бы равенство
получилось бы равенство
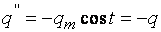
Чтобы в выражении второй производной 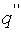 был множитель
был множитель  запишем уравнение (1) в виде:
запишем уравнение (1) в виде:
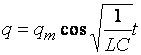 (2)
(2)
Найдем первую и вторую производные:
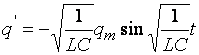


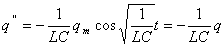
Функция (2) есть решение исходного уравнения (1). Функция
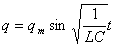 есть также решение исходного уравнения.
есть также решение исходного уравнения.
Обозначим постоянную величину 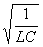 , зависящую от свойств системы, через
, зависящую от свойств системы, через 
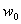 :
: 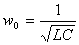
Тогда решение уравнения (2) можно записать:
 (3)
(3)
Тогда уравнение (1), описывающее свободные электромагнитные колебания примет вид:
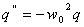 (4)
(4)
Из курса математики известно, что наименьший период косинуса равен 2π. Следовательно, ω0=2π,
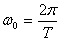 . Так как
. Так как 
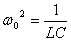 , тогда период колебаний равен
, тогда период колебаний равен
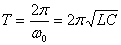 - формула Томсона.
- формула Томсона.
Аналогично этим рассуждениям решим уравнение для колебаний вертикального пружинного маятника:
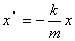 (5)
(5)
Запишем уравнение (5) в виде:
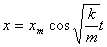 (6)
(6)
Найдем первую и вторую производные:
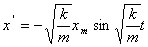
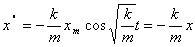
Функция (6) есть решение исходного уравнения. Функция 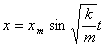 есть также решение исходного уравнения. Обозначим постоянную величину
есть также решение исходного уравнения. Обозначим постоянную величину
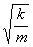 через w0 получим
через w0 получим
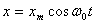 (7)
(7)
Тогда уравнение (5) будет иметь вид:
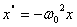 (8)
(8)
Период колебаний для пружинного маятника по аналогии с формулой Томсона
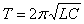
где 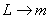 ;
; 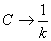 получим
получим
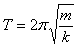 (9)
(9)
Аналогично выше изложенным рассуждениям решим уравнение для колебаний математического маятника:
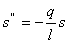 (10)
(10)
Запишем уравнение (10) в виде:
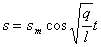 (11)
(11)
Найдем первую и вторую производные уравнения (11):
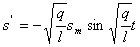
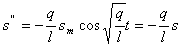
Функция (11) есть решение уравнения (10). Обозначим постоянную величину 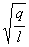 ,зависящую от свойств системы, через w0 получим:
,зависящую от свойств системы, через w0 получим:
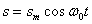 (12)
(12)
Тогда уравнение (10) примет вид:
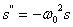 (13)
(13)
По аналогии с формулой(8) и формулой Томсона, для математического маятника период колебаний равен:
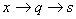 ;
; 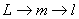 ;
; 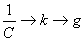
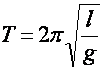 (14)
(14)
Уравнения (4), (8) и (13) являются решениями уравнений, описывающих колебания в пружинном и математическом маятникам.
§ 3 Решение физических задач.
Рассмотрим несколько задач, решение которых методом аналогии возможно на уроках и факультативных занятиях в 11 классах (после изучения раздела "Электрические колебания) и при повторении материала.
Задача1. Изобразите механические системы, аналогичные электрическим цепям, схематически изображенными на рис.1,а,б
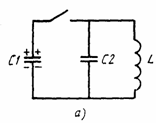
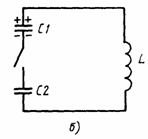
Решение. Аналогичная механическая система соответствующая рис.1,а,б должна содержать тело массой m и две пружины с разными жестокостями 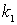 и
и 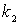
а) Общая емкость системы конденсаторов (рис.1,а) равна
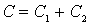
Используя аналогию механических и электрических величин, найдем что общая жесткость пружин искомой механической системы находится из соотношения

Это соответствует последовательному соединению двух пружин. Учитывая, что один конденсатор заряжен, искомую механическую систему можно представить в виде одной сжатой пружины жесткость 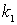 и одной недеформированной пружины жесткостью
и одной недеформированной пружины жесткостью 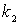 (рис.2,а).
(рис.2,а).
б) Аналогично рассмотрим вторую схему.
Общая емкость системы конденсаторов (рис.1,б) равна

Используя аналогию механических и электрических величин, найдем что общая жесткость пружин искомой механической системы находится из соотношения
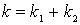
Это соответствует параллельному соединению двух пружин(рис.2,б).
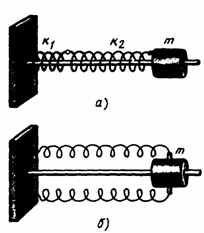 рис.2.
рис.2.
Задача2На рис.3,а,б изображены колебательные контуры. Придумайте механические аналоги им.
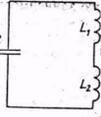
рис.3,а
О т в е т. Аналогичная механическая система соответствующая рис.3,а,б должна содержать два тела массами 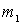 и
и 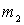 , и пружину жесткостью k.
, и пружину жесткостью k.
а) Общая индуктивность системы при последовательном соединении катушек равна
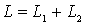
Используя аналогию механических и электрических величин найдем, что общая масса
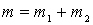
А это соответствует рис.4,а
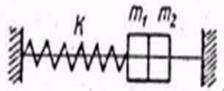
Рис. 4.а
б) Аналогично рассматриваем вторую схему.
Общая индуктивность параллельно соединенных катушек находится из соотношения