Избыточные коды

Страница 2

где I- единичная kXk подматрица, P-kX(n-k)- подматрица проверочных символов, определяющая свойства кода. Матрица задает систематический код. Можно показать, что для лю­бого линейного кода существует эквивалентный систематический код.

Линейный (п, k) код может быть задан про­верочной матрицей Н размерности (rХп). При этом комбинация В принадлежит коду только в том случае, если вектор В ортого­нален всем строкам матрицы Н, т. е. если выполняется равенство (7.9)

где т—символ транспонирования матрицы. Так как это равенство справедливо для любой кодовой комбинации, то

Каноническая форма матрицы Н имеет вид (7.10)

где P - подматрица, столбцами которой служат строки подмат­рицы Р (7.8), I-единичная rXr подматрица. Подставляя (7.10) в (7.9), можно получать п—k уравнений вида (7.11)

которые называются уравнениями проверки. Из (7.11) следует, что проверочные символы кодовых комбинаций линейного кода образуются различными линейными комбинациями информаци­онных символов. Единицы в любой j-й строке подматрицы Р, входящей в проверочную матрицу (7.10), указывают, какие информационные символы участвуют в формировании j-го провероч­ного символа.

Очевидно, что линейный (п, k) код можно построить, исполь­зуя уравнения проверки (7.11). При этом первые k символов ко­довой комбинации информационные, а остальные п-k симво­лов - проверочные, образуемые в соответствии с (7.11).

С помощью проверочной матрицы сравнительно легко можно построить код с заданным кодовым расстоянием. Это построение основано на следующей теореме: кодовое расстояние линей­ного (п, k) кода равно d тогда и только тогда, когда любые d-1 столбцов проверочной матрицы этого кода линейно независимы, но некоторые d столбцов проверочной матрицы линейно зависимы.

Заметим, что строки проверочной матрицы линейно независи­мые. Поэтому проверочную матрицу можно использовать в ка­честве порождающей для некоторого другого линейного кода (п, п-k), называемого двойственным.

Кодирующее устройство для линейного (п,k) кода (рис. на предыдущей стр.) состоит из k-разрядного сдвигающего регистра и r=п-k бло­ков сумматоров по модулю 2. Информационные символы одно­временно поступают на вход регистра и на выход кодирующего устройства через коммутатор К. С поступлением k-го информаци­онного символа на выходах блоков сумматоров в соответствии с уравнениями (7.11) формируются проверочные символы, которые затем последовательно поступают на выход кодера. Процесс декодирования сводится к выполнению операции

, где S — вектор размерностью (п-k), называемый синдромом, В- вектор принятой кодовой комбинации. Если принятая комбинация В совпадает с одной из разрешенных В (это имеет место тогда, когда либо ошибки в принятых символах отсутствуют, либо из-за действия помех одна разрешенная кодовая комбинация переходит в другую), то В противном случае S≠O, причем вид синдрома зависит только от вектора ошибок е. Действительно,

где В- вектор, соответствующий передаваемой кодовой комби­нации. При S=0 декодер принимает решение об отсутствии оши­бок, а при S≠O - о наличии ошибок. По конкретному виду синдрома можно в пределах кор­ректирующей способности кода указать на ошибочные символы и их исправить.

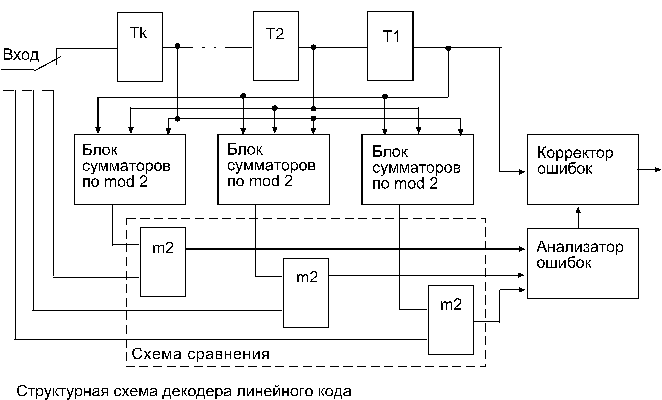
Декодер линейного кода (рис. на следующей стр.) состоит из k- разрядного сдвигающего регистра, (п-k) блоков сумматоров по модулю 2, схе­мы сравнения, анализатора ошибок и корректора. Регистр слу­жит для запоминания информационных символов принятой кодо­вой последовательности, из которых в блоках сумматоров формируются проверочные символы. Анализатор ошибок по конкретно­му виду синдрома, получаемого в результате сравнения формиру­емых на приемной стороне и принятых проверочных символов, оп­ределяет места ошибочных символов. Исправление информацион­ных символов производится в корректоре. Заметим, что в общем случае при декодировании линейного кода с исправлением ошибок в памяти декодера должна храниться таблица соответствий между синдромами и векторами ошибок. С приходом каждой кодовой комбина­ции декодер должен перебрать всю таблицу. При небольших зна­чениях (п-k) эта операция не вызывает затруднений. Однако для высокоэффективных кодов длиной п, равной нескольким десяткам, разность (п-k) принимает такие значения, что перебор таблицы оказывается практически невозможным. Например, для кода (63, 51), имеющего кодовое расстояние d=5, таблица состоит из 2^12 = 4096 строк.

Задача заключается в выборе наилучшего (с позиции то­го или иного критерия) кода. Следует заметить, что до сих пор общие методы синтеза оптимальных линейных кодов не разра­ботаны.

Циклические коды.

Циклические коды относятся к классу линейных системати­ческих. Поэтому для их построения в принципе достаточно знать порождающую матрицу.

Можно указать другой способ построения циклических кодов, основанный на представлении кодовых комбинаций многочлена­ми b(х) вида:

где bn-1bn-2 .bo - кодовая комбинация. Над данными много­членами можно производить все алгебраические действия с уче­том того, что сложение здесь осуществляется по модулю 2.

Каждый циклический код (n, k) характеризуется так назы­ваемым порождающим многочленом. Им может быть любой мно­гочлен р(х) степени n-k. Циклические коды характеризуются тем, что многочлены b(x) кодовых комбинаций делятся без остатка на р(х). Поэтому процесс кодирования сводится к отысканию многочлена b(x) по известным многочленам a(х) а р(х), делящегося на р(х), где a(х)- многочлен степени k-1, соответствующий информацион­ной последовательности символов.

Очевидно, что в качестве многочлена b(x) можно использо­вать произведение a(х)р(х). Однако при этом информационные и проверочные символы оказываются перемешанными, что затруд­няет процесс декодирования. Поэтому на практике в основном применяется следующий метод нахождения многочлена b(x). Умножим многочлен а(х) на и полученное произведение разделим на р(х). Пусть (7.12)