Aлгоритмы на графах

Страница 2

End;

Begin

write('A= '); readln(A);

write('B= '); readln(B);

A_to_B(A, B)

End.

Эйлеровы циклы.

Требуется найти цикл, проходящий по каждой дуге ровно один раз. Эту задачу впервые поставил и решил Леонард Эйлер, чем и заложил основы теории графов, а соответствующие циклы теперь называются эйлеровыми.

Задача возникла из предложенной Эйлеру головоломки, получившей название "проблема кенигсбергских мостов". Река Прегель, протека ющая через Калининград (прежде город назывался Кенигсбергом), омывает два острова. Берега реки связаны с островами так, как это показано на рисунке. В головоломке требовалось найти маршрут, проходящий по всем участкам суши таким образом, чтобы каждый из мостов был пройден ровно один раз, а начальный и конечный пункты маршрута совпадали.

Выберем в качестве вершин графа берега реки, а в качестве ребер - мосты, их соединяющие. После этого задача становится очевидной: требование неосуществимо - чтобы его выполнить, число дуг, приходящих к каждой вершине, должно быть четным. В самом деле, поскольку по одному мосту нельзя проходить дважды, каждому входу на берег должен соответствовать выход.

Что необходимо, чтобы в графе существовал эйлеров цикл? Во-первых, граф должен быть связанным: для любых двух вершин должен существовать путь, их соединяющий. Во-вторых, для неориентированных графов число ребер в каждой вершине должно быть четным. На самом деле этого оказывается достаточно.

Теорема. Чтобы в связанном графе существовал эйлеров цикл, необходимо и достаточно, чтобы число ребер в каждой вершине было четным.

Доказательство. Необходимость доказана выше. Доказательство достаточности конструктивно - в результате будет получен требуемый алгоритм.

Доказательство ведется индукцией по числу ребер графа. Пусть утверждение доказано для всех m<n. Рассмотрим граф с n ребрами. Выберем произвольную вершину A и начнем строить требуемый путь, вычерчивая (стирая) каждое ребро, по которому проходим, чтобы не

пройти его дважды.

Заметим, что, пока мы не вернулись в А, мы всегда можем продолжить путь из текущего узла X по крайней мере на одно ребро. В самом деле, каждый проход через X оставляет четным число ребер в этой вершине. Поэтому, если мы входим в X, остается нечетное число невычеркнутых ребер, из нее выходящих (по крайней мере одно ребро). Пусть мы вернулись в A. Тогда, если все ребра вычеркнуты, теорема доказана. В противном случае оставшиеся ребра распадаются на связанные подграфы, каждый из которых содержит хотя бы одну вершину из уже построенного цикла (поскольку первоначальный граф связанный) и содержит менее n ребер. Пусть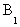, …,– вершины указанных подграфов, через которые проходит построенный путь.

По предположению индукции в каждом из них существует эйлеров цикл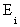. Строим теперь новый путь из A следующим образом:

– идем по старому пути до ;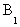

– включаем в него новый путь ;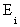

– идем по старому пути от 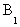до ;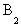

– повторяем процесс для вершины 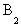и т.д.

Для окончания доказательства (и построения алгоритма) заметим, что база индукции очевидна: если ребро одно, то оно – петля.

Хотя доказательство проведено для неориентированных графов, оно сразу переносится на ориентированные, только требование четности заменяется теперь на такое: число входящих в каждую вершину ребер должно быть равно числу выходящих.

Осталось заметить, что предложенный в доказательстве алгоритм линеен, т.е. число действий прямо пропорционально числу ребер.

Program Euler;

const n=9;

m: array[1 n, 1 n] of boolean=

(

(False, True, True, False, False, False, False, False, False),

(True, False, True, False, False, False, True, True, False),

(True, True, False, True, True, False, False, False, False),

(False, False, True, False, True, False, False, False, False),

(False, False, True, True, False, True, False, True, False),

(False, False, False, False, True, False, True, True, True ),

(False, True, False, False, False, True, False, True, True ),

(False, True, False, False, True, True, True, False, False),

(False, False, False, False, False, True, True, False, False)

);

Type

list=^node;

node=record

i: integer;

next: list

end;

Var stack1, stack2: list;

v, u, x, i: integer;

Procedure Push(x: integer; var stack: list);

Var temp: list;

Begin

New(temp);

temp^.i:=x;

temp^.next:=stack;

stack:=temp

End;

Procedure Pop(var x: integer; var stack: list);

Begin

x:=stack^.i;

stack:=stack^.next

End;

Function Peek(stack: list): integer;

Begin

Peek:=stack^.i

End;

Procedure PrintList(l: list);

Begin

Writeln;

If l=nil then writeln('NIL');

While l<>nil do

Begin

Write(l^.i:3);

l:=l^.next

End

End;

Begin

stack1:=nil;

stack2:=nil;

Write('Начальная вершина: ');readln(v);

Push(v, stack1);

While stack1<>NIL do

Begin

v:=peek(stack1);

i:=1;

While (i<=n) and not m[v, i] do inc(i);

If i<=n then

Begin

u:=i;

Push(u, stack1);

m[v, u]:=False;

m[u, v]:=False;

End

else

Begin

pop(x, stack1);

push(x, stack2)

End

End;

PrintList(stack2)

End.

Задача Прима–Краскала.

Дана плоская страна и в ней n городов. Нужно соединить все города телефонной связью так, чтобы общая длинна телефонных линий была минимальной.

Или в терминах теории графов:

Дан граф с n вершинами; длины ребер заданы матрицей. Найти остовное дерево минимальной длины.

Представим себе, что зимовщику оставлен некоторый запас продуктов, и его задачей является составление вкусного меню на всю зиму. Если зимовщик начнет с того, что сперва будет есть самую вкусную еду (например, шоколад), потом – вторую по вкусности (например, мясо), то он рискует оставить на последний месяц только соль и маргарин. Подобным образом, если оптимальный (для определенности, минимальный) объект строится как-то по шагам, то нельзя на первом шаге выбирать что-нибудь самое малое, на втором шаге – оставшееся самое малое и т.д. За такую политику обычно приходится расплачиваться на последних шагах. Такой алгоритм называется жадным.

Удивительно, но в задаче Прима–Краскала, которая не кажется особенно простой, жадный алгоритм дает точное оптимальное решение.

Как известно (это легко доказать по индукции), дерево с n вершинами имеет n-1 ребер. Оказывается, каждое ребро нужно выбирать жадно (лишь бы не возникали циклы). То есть n-1 раз выбирать самое короткое ребро из еще не выбранное ребро при условии, что оно не образует цикла с уже выбранными.

А как следить, чтобы новое ребро не образовывало цикла со старыми? Сделать это просто. До построения дерева окрасим каждую вершину i в отличный от других цвет i. При выборе очередного ребра, например (i, j), где i и j имеют разные цвета, вершина j и все, окрашенные в ее цвет (т.е. ранее с ней соединенные) перекрашиваются в цвет i. Таким образом, выбор вершин разного цвета обеспечивает отсутствие циклов. После выбора n-1 ребер все вершины получают один цвет.

Докажем, что описанный алгоритм получает в точности минимальное решение. Для доказательства нам понадобится очень простое утверждение:

Если к дереву добавить ребро, то в дереве появится цикл, содержащий это ребро.

Действительно, пусть добавлено ребро (u, v) – “добавлено” означает, что ребро – новое, что раньше его в дереве не было. Поскольку дерево является связанным графом, то существует цепь C(u, …, v) из нескольких ребер, соединяющая вершины u и v. Добавление ребра (u, v) замыкает цепь, превращая ее в цикл.