Aлгоритмы на графах

Страница 4

1 (инициализация). В цикле от 1 до n заполнить значением False массив Visited; заполнить числом i массив C (i – номер стартовой вершины); перенести i-ю строку матрицы Matrix в массив Len;

Visited[i]:=True; C[i]:=0;

2 (общий шаг). Найти минимум среди неотмеченных (т.е. тех к, для которых Visitid[k]=False); пусть минимум достигается на индексе j, т.е. Len[j]£Len[k];

Затем выполнять следующие операции:

Visited[i]:=True;

если Len[k]>Len[j]+Matrix[j, k], то (Len[k]:=Len[j]+Matrix[j, k]; C[k]:=j)

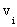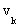{Если все Visited[k] отмечены, то длина пути от до равна C[k]. Теперь надо перечислить вершины, входящие в кратчайший путь}.

3 (выдача ответа). {Путь от 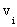до 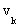выдается в обратном порядке следующей процедурой:}

3.1 z:=C[k];

3.2 Выдать z

3.3 z:=C[z]. Если z =0, то конец,

иначе перейти к 3.2.

Теорема. Алгоритм Дейкстры – корректен.

Доказательство. Теорему докажем по индукции. Рассмотрим 1-й шаг, когда находится min Len[k] (k¹i), пусть минимум достигается на вершине j. Остальные 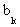(k¹i, j) пока лишь верхние оценки длин путей из 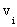в 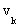(они могут уменьшаться в ходе выполнения алгоритма, но Len[j] – окончательная длина пути [ 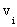… ], совпадающего с дугой [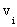, ]. Если бы существовал путь короче, он бы выглядел [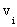, 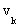…], но уже первая его дуга не меньше, чем весь путь [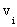, ], а остальные дуги имеют положительную длину).

Мы разбили все вершины на два класса: С – неотмеченных вершин и С’ – отмеченных вершин. После 1-го общего шага 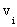, Î С’, и, очевидно, все кратчайшие пути (пока “все” – означает “один”) из v’ÎС’ не содержат vÎС в качестве промежуточной.

Теперь сделаем индуктивный шаг. Уже проделано s общих шагов, уже С’={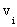, , 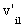, 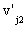…, 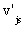}, при этом все кратчайшие пути из 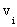в v’ не содержат вершин из С в качестве промежуточных.

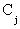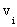Найдем минимальное Len[l] в неотмеченных столбцах; пусть минимум достигается на вершине . Соответственный элемент , меняясь, мог принимать только номера отмеченных вершин, значит в вершину идет путь, где все вершины, кроме конечной , – штрихованные, т.е. принадлежащие С’. Любой другой путь [ … ], содержащий хотя бы еще одну не штрихованную вершину, будет длиннее. Теорема доказана.

Uses Crt;

Const MaxSize=10;

Infinity=1000;

Var Mattr: array [1 MaxSize, 1 MaxSize] of integer;

Visited: array [1 MaxSize] of boolean;

Len,Path: array [1 MaxSize] of integer;

n, Start, Finish, k, i: integer;

Procedure Init;

Var f: text;

i, j: integer;

Begin

Assign(f, INPUT.MTR');

Reset(f);

Readln(f, n);

For i:=1 to n do

Begin

For j:=1 to n do Read(f, mattr[i,j]);

Readln(f)

End;

Write('Начальная вершина: '); Readln(Start);

For i:=1 to n do

Begin

Visited[i]:=False;

Len[i]:=Mattr[Start, i];

Path[i]:=Start

End;

Path[Start]:=0;

Visited[Start]:=True

End;

Function Possible: Boolean;

Var i: integer;

Begin

Possible:=True;

For i:=1 to n do If not Visited[i] then Exit;

Possible:=False

End;

Function Min: Integer;

Var i, minvalue, currentmin: integer;

Begin

Minvalue:=Infinity;

For i:=1 to n do

If not Visited[i] then

If Len[i]<minvalue then

Begin

currentmin:=i;

minvalue:=Len[i]

End;

min:=currentmin

End;

Begin

ClrScr;

Init;

While Possible do

Begin

k:=min;

Visited[k]:=True;

For i:=1 to n do

If Len[i]>Len[k]+Mattr[i, k] then

Begin

Len[i]:=Len[k]+Mattr[i, k];

Path[i]:=k

End

End;

Write('Конечная вершина: '); Readln(Finish);

Write(Finish);

Finish:=Path[Finish];

While Finish<>0 do

Begin

Write('<-', Finish);

Finish:=Path[Finish];

End;

ReadKey

End.

Например, для сети, описанной в предыдущей главе, кратчайший путь из 3-ей вершины в 8-ю будет: 8¬2¬3.