Автоматизация процесса спекания аглошихты
Страница 12
Чертежи монтажно-коммутационных схем щитов необходимы для выполнения электрической и трубной коммутации приборов и средств автоматизации в пределах щита. Монтажные схемы выполняют в виде отдельных чертежей для каждой панели щита.
В графической части дипломного проекта (лист 7) выполнен чертеж панели №4. На этой схеме отображаются клеммники на десять клемм для соединения приборов между собой и клеммники на 6 клемм для подсоединения питающего напряжения. Приборы на монтажно-коммутационной схеме размещаются так, как они будут размещены на обратной стороне щита. Линии и связи нумеруются так же, как и на принципиально-электрической схеме. Отображается без масштаба.
6.7 Математическая модель
6.7.1 Разработка детерминированной математической модели
Физико-математические модели агломерационного процесса могут быть получены аналитически, путем последовательного описания физических и химических превращений в исходных материалах в процессе производства [21]. Динамическая математическая модель спекания агломерационной шихты, реализуемая на ЭВМ, позволяет быстро и с минимальными затратами исследовать влияние ведущих параметров процесса спекания (высоты слоя шихты, содержания углерода и влаги в шихте, скорости движения спекательных тележек и др.) на его технико-экономические показатели и может быть использована в качестве информационной части в АСУ агломерационным
производством для оптимизации технологического процесса. Алгоритм динамического моделирования в математической форме отражает физико-химические превращения и тепловые явления в спекаемом слое шихты практически в той мере, в какой процесс агломерации в настоящее время может быть описан аналитически.
В алгоритм динамической модели процесса спекания включены зажигание, сушка (переувлажнение) шихты, горение топлива, нагрев и охлаждение слоя шихты, изменение расхода газов, плотности шихты, теплоемкости материалов и газов, коэффициентов тепло- и влагообмена по ходу технологического процесса. Некоторые химические (в том числе минералогические) превращения в настоящее время исследованы и описаны недостаточно полно, поэтому их влияние на процесс можно учесть только приблизительно, путем некоторой коррекции теплофизических свойств шихты и агломерата, материального баланса и других хорошо изученных факторов.
Математическая модель основана на следующих предпосылках. Ввиду малых размеров частиц шихты их температура постоянна по объему; все частицы элементарного объема шихты, расположенные на одном горизонте слоя, имеют одинаковую температуру; тепловые эффекты реакций локализованы в объеме частиц шихты; теплообмен между шихтой и газовым потоком происходит при граничных условиях третьего рода; теплообмен теплопроводностью или излучением между слоями шихты, расположенными на различных горизонтах, отсутствует; теплота плавления и кристаллизации выражена зависимостью теплоемкости материалов от температуры; теплоемкости шихты и агломерата одинаковы; теплота экзо- и эндотермических реакций, а также потери теплоты с механическим недожогом и в окружающую среду определяются путем коррекции тепловыделения при горении коксика (по тепловому балансу); кислород диссоциирующих оксидов рассчитывается по уравнению, в котором содержание кислорода в воздухе корректируют с помощью коэффициентов (по материальному балансу); аккумуляцией теплоты и массы газами в слое можно пренебречь, так как она мала по сравнению с аккумуляцией теплоты и массы материалами; теплоемкость газов не зависит от их состава. Многие из этих допущений не влияют сколько-нибудь существенно на структуру алгоритма моделирования.
В слое спекаемой агломерационной шихты протекают процессы горения топлива, тепло- и влагообмена; изменяются давления водяных паров в газах, насыпная плотность шихты, теплоемкость шихтовых материалов, агломерата и продуктов сгорания. Некоторые из этих физических и химических явлений математически могут быть охарактеризованы системой алгебраических уравнений, не содержащих пространственной координаты и времени. Действительно, зависимости коэффициента теплоотдачи от температуры и состава шихты или теплоемкости газов от температуры сохраняются в любом месте слоя в любой момент времени. Это же относится и к другим подобным зависимостям. Рассмотрим алгебраические уравнения модели.
При горении топлива выделяется теплота:
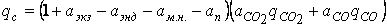 , (6.7.1)
, (6.7.1)
где 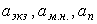 - тепловые эффекты экзо- и эндотермических реакций, потери с механическим недожогом и в окружающую среду, выраженные в долях от теплоты сгорания;
- тепловые эффекты экзо- и эндотермических реакций, потери с механическим недожогом и в окружающую среду, выраженные в долях от теплоты сгорания;
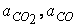 - доля углерода, сгорающего до СО2 и СО;
- доля углерода, сгорающего до СО2 и СО;
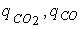 - теплоты сгорания углерода до СО2 и СО.
- теплоты сгорания углерода до СО2 и СО.
Совместное протекание тепло- и влагообмена в слое характеризуется психрометрическим коэффициентом:
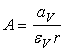 , (6.7.2)
, (6.7.2)
Здесь 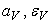 - объемные коэффициенты теплоотдачи и влагообмена;
- объемные коэффициенты теплоотдачи и влагообмена;
r — теплота парообразования.
Коэффициент теплоотдачи между газами и шихтой зависит от скорости и температуры газов и уменьшается в процессе сушки и спекания шихты, поэтому можно записать:
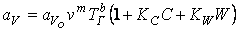 , (6.7.3)
, (6.7.3)
где v - скорость продуктов сгорания в свободном сечении слоя;
ТГ - абсолютная температура газа;
С - содержание углерода в шихте;
W - влажность шихты;
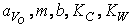 - постоянные.
- постоянные.
Давление насыщенных водяных паров в продуктах сгорания Рнас зависит от температуры шихты tш и величины нормального давления Рн:
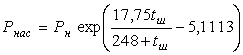 (6.7.4)
(6.7.4)
Парциальное давление водяных паров в газах Рв.п. можно выразить через парциальную скорость 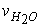 и абсолютное давление продуктов сгорания Р:
и абсолютное давление продуктов сгорания Р:
Рв.п = Р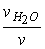 (6.7.5)
(6.7.5)
Насыпная плотность шихты 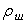 зависит от ее абсолютной плотности
зависит от ее абсолютной плотности 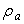 и пористости П:
и пористости П:
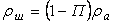 (6.7.6)
(6.7.6)
Если допустимо некоторое уменьшение точности моделирования, то можно принять 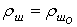 = const. Для расчетов повышенной точности может быть использована величина усадки шихты, зависящая от разрежения в вакуум-камерах, высоты слоя и других факторов. На теплоемкость шихтовых материалов Сш и газов С влияет температура шихты tш и газов tг:
= const. Для расчетов повышенной точности может быть использована величина усадки шихты, зависящая от разрежения в вакуум-камерах, высоты слоя и других факторов. На теплоемкость шихтовых материалов Сш и газов С влияет температура шихты tш и газов tг:
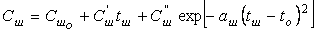 (6.7.7)
(6.7.7)
С = Сг.о + C'г fг, (6.7.8)
где 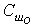 ,
,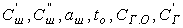 - постоянные.
- постоянные.
Продукты сгорания, проходящие через спекаемый слой, состоят из кислорода, водяных паров и других газов, поэтому парциальные скорости связаны соотношением:
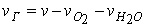 (6.7.9)
(6.7.9)
Физические и химические превращения в спекаемом слое агломерационной шихты протекают во времени τ и в пространстве (по высоте слоя, пространственная координата Z). Эти динамические процессы (сушка, горение углерода, изменение температуры, концентрации кислорода в газах, парциальной скорости водяных паров и кислорода по высоте слоя) характеризуются системой дифференциальных уравнений в частных производных по τ и Z. Скорость сушки шихты (или ее переувлажнения) пропорциональна разности относительных давлений водяных паров: по выражению (6.7.4) — для насыщенных паров, по уравнению (6.7.5) — для действительных значений ненасыщенных.