Автоматизация процесса спекания аглошихты
Страница 13
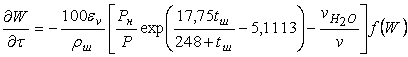 (6.7.10)
(6.7.10)
В процессе сушки влага мигрирует внутри частиц шихты, поэтому влажность последней необходимо учитывать:
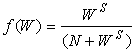 , (6.7.11)
, (6.7.11)
где S, N — постоянные.
Эксперименты по динамике сушки агломерационной шихты показали, что N = 5,64 и S = 1,13, если W выражена в процентах на сухую массу. Для процесса переувлажнения f(W) = 1, так как в этом случае миграция влаги в частицах шихты на скорости процесса не отражается. Из уравнения материального баланса влаги следует
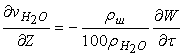 , (6.7.12)
, (6.7.12)
где 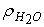 - плотность водяных паров.
- плотность водяных паров.
Исследования горения углерода в слое показали, что градиент концентрации кислорода в газах по высоте слоя сложным образом зависит от параметров процесса — концентрации кислорода в газе 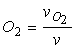 , среднего радиуса частицы топлива Rc, плотности топлива
, среднего радиуса частицы топлива Rc, плотности топлива 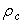 и др.:
и др.:

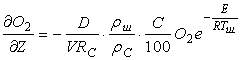 , (6.7.13)
, (6.7.13)
где D, R, E — постоянные.
Так как текущие значения Rc и С связаны с начальными значениями 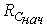 и
и 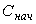 соотношением
соотношением 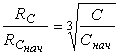 , то
, то
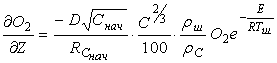 (6.7.14)
(6.7.14)
На основании уравнения (6.7.14) с учетом материального баланса кислорода и углерода можно записать уравнение скорости горения углерода:
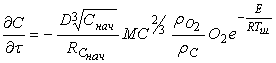 , (6.7.15)
, (6.7.15)
где 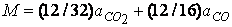 - стехиометрический коэффициент;
- стехиометрический коэффициент;
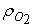 - плотность кислорода.
- плотность кислорода.
Из уравнений (6.14) и (6.15) получаем выражение изменения парциальной скорости кислорода по высоте слоя:
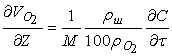 (6.7.16)
(6.7.16)
Составив уравнение теплового баланса газового потока, найдем градиент температуры газов по высоте слоя 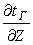 и скорость изменения температуры шихты
и скорость изменения температуры шихты 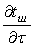 :
:
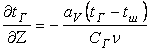 (6.7.17)
(6.7.17)
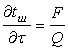 (6.7.18)
(6.7.18)
При этом
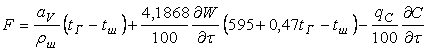 ; (6.7.19)
; (6.7.19)
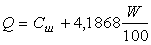 (6.7.20)
(6.7.20)
Уравнения (6.7.1) – (6.7.18) являются аналитической основой математического динамического моделирования агломерационного процесса на ЭВМ. Расчетная схема модели спекаемого слоя представлена на рисунке 6.7.1.
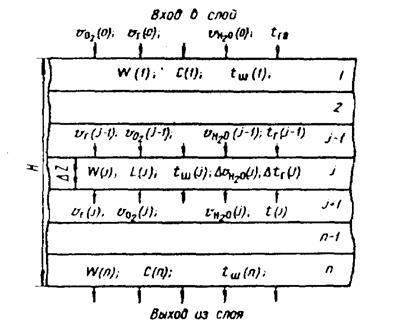
Рис. 6.7.1 - Расчетная схема модели спекаемого
слоя агломерационной шихты
Слой шихты высотой Н разбит на n зон, так что ∆Z=H/n. Слои пронумерованы по ходу процесса спекания (сверху вниз): 1, 2, … , j –1 , j , j + 1, … , n – 1, n. Дискретизация процесса моделирования во времени с шагом дискретности ∆τ позволяет производить расчеты по шагам, номера которых 1, 2, … , К – 1, К, К + 1, … . В результате квантования процесса во времени и в пространстве ∆Z дифференциальные уравнения (6.7.11) – (6.7.18) представлены в конечно-разностной форме. Запишем итерационную схему функционирования динамической модели. Для величин, относящихся к шихте (W, C, tш), например, для влажности: 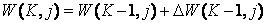 , а для величин, относящихся к газовому потоку
, а для величин, относящихся к газовому потоку 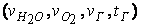 , например для скорости водяных паров:
, например для скорости водяных паров:
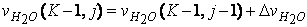 (6.7.21)
(6.7.21)
Для шихты номер j соответствует элементу разбиения; для газового потока номер j – 1 означает вход в элементарный слой с номером j, а номер j – выход из него.
Перейдем в дифференциальных уравнениях (6.7.10) - (6.7.18) к конечным разностям (от 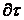 к
к 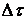 и от
и от 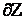 к
к 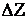 ) и выберем
) и выберем 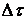 и
и 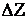 достаточно малыми. Тогда приращения
достаточно малыми. Тогда приращения 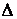 величин W, C,
величин W, C, 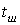 ,
, 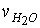 ,
, 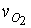 ,
, 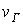 и
и 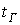 можно представить в виде:
можно представить в виде:
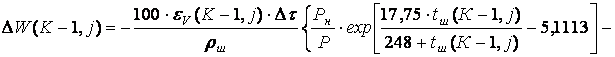
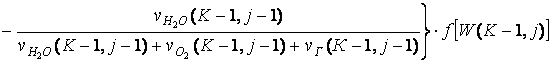 ; (6.7.22)
; (6.7.22)
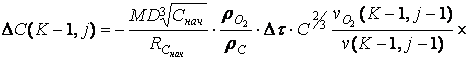
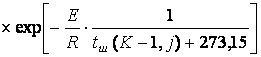 ; (6.7.23)
; (6.7.23)
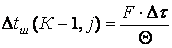 ; (6.7.24)
; (6.7.24)
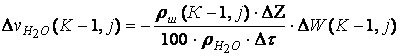 ; (6.7.25)
; (6.7.25)
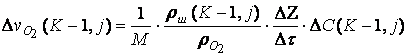 ; (6.7.26)
; (6.7.26)
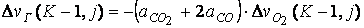 ; (6.7.27)
; (6.7.27)
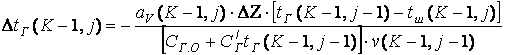 , (6.7.28)
, (6.7.28)
где
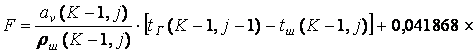
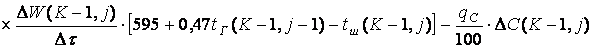 ;
;
(6.7.29)
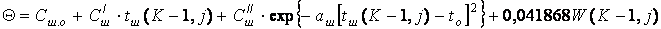 (6.7.30)
(6.7.30)
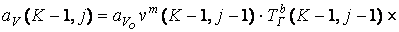
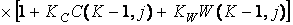 ; (6.7.31)
; (6.7.31)
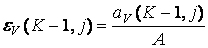 (6.7.32)
(6.7.32)
Изменение скорости просасываемого через слой воздуха 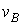 при моделировании принято таким же, как и в производственных условиях, в которых установлена эмпирическая зависимость (парабола четвертой степени):
при моделировании принято таким же, как и в производственных условиях, в которых установлена эмпирическая зависимость (парабола четвертой степени):
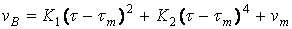 , (6.7.33)
, (6.7.33)
где 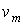 - минимальный расход в момент времени
- минимальный расход в момент времени 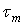 ;
;
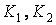 - постоянные.
- постоянные.
В процессе программирования расчетов на ЭВМ предусмотрены логические операции по ограничению величин С≥0 и W≥0 это позволяет обеспечить абсолютную устойчивость процесса вычислений.
6.7.2 Выбор входных и выходных параметров
Моделирование выполняется на ЭВМ при следующих условиях:
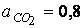 ;
; 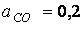 ;
; 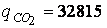 кДж/кг;
кДж/кг; 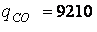 кДж/кг;
кДж/кг;
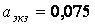 ;
; 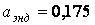 ;
; 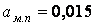 ;
; 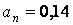 ;
; 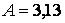 К;
К;