Механизмы качающегося конвейера

Страница 3

1.5. Определение приведенного момента инерции и момента инерции маховика.

За звено приведения принимается входное звено (кривошип ОА) рычажного механизма. Для каждого положения механизма приведенный момент инерции звеньев находится по формуле:

,

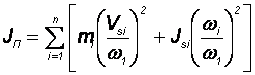где mi – масса звена i, Jsi – момент инерции звена i относительно оси, проходящей через центр масс Si звена, wi – угловая скорость звена i, Vsi – скорость центра масс звена i.

Рассчитаем Jп для первого положения механизма:

Аналогично рассчитываем Jп для каждого положения, результаты расчетов заносим в таблицу 4.

Таблица 4.

	Положения механизма
1	2	3	4	5	6	7	8	9	10	11	12
Jп	кгÄм2	1,2	7,7	12,21	10,84	7,12	3,91	1,98	1,2	2,55	10,37	30,76	19,01

Строим график момента сил сопротивления. Назначаем масштабные коэффициенты:

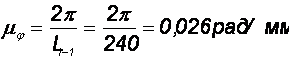
где L1-1 – длина координат абсцисс, мм

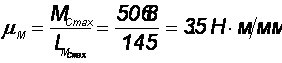
Откладываем значения моментов сил сопротивления и соединяем точки кривой.

Строим график изменения работ сил сопротивления и движущих сил. График строится путем интегрирования графика моментов сил сопротивления, отмечаем соответствующие точки и соединяем их кривой, которая будет графическим аналогом работы сил сопротивления АС. Первую и последнюю точки графика соединяем прямой, которая будет графическим аналогом работы движущих сил АД. Путем обратного интегрирования переносим эту прямую на график моментов сил сопротивления, которая будет графическим аналогом движущего момента МД.

Строим график изменения кинетической энергии. Находим изменение кинетической энергии на каждом участке, оно равняется разности работ приведенных моментов движущих сил и сил сопротивления на каждом участке Аизб=АД-АС. Откладываем полученные значения но оси ординат для каждого положения и соединяем их кривой, которая будет графическим аналогом изменения кинетической энергии.

Строим график приведенных моментов инерции JП. Для построения графика ось ординат направляем горизонтально, т.е. поворачиваем график на 900. Принимаем масштабный коэффициент:

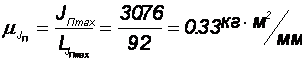
Стоим график приведенного момента инерции.

Строим диаграмму «энергия – масса» путем графического исключения параметра j из графиков изменения кинетической энергии механизма и приведенного момента инерции.

Для определения момента инерции маховика по заданному коэффициенту неравномерности движения d проводим касательные к графику «энергия – масса» под углами ymax и ymin к оси абсцисс, тангенсы которых определяются по формулам:

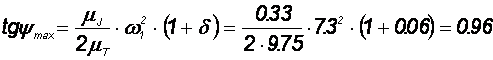
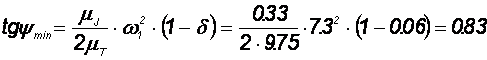
Определяем углы ymax и ymin : ymax = 43,7Å ymax = 40,3Å.

Проводим касательные прямые под полученными углами. В местах пересечения этих прямых с осью абсцисс ставим точки k и l.

Искомый момент инерции маховика определяется по формуле:

,

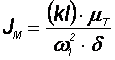где kl – отрезок, отсекаемый проведенными касательными.

Момент инерции маховика:

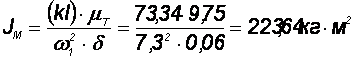
2. Динамический анализ рычажного механизма

При динамическом анализе определяются реакции в кинематических парах механизма и уравновешивающий момент, приложенный к начальному звену, от действующих внешних сил и сил инерции.

2.1. Исходные данные.

Схема положения механизма (Рисунок 2.)

Таблица 5.

Размеры звеньев рычажного механизма	Положение кривошипа при силовом расчете	Массы звеньев механизмов
ОА	AB	BC	BD	f1	m2	m3	m4	m5
м	м	м	М	град	кг	кг	кг	Кг
0.12	0.46	0.39	1.5	120	18	20	100	500

Продолжение таблицы5

Момента инерции звеньев	Сила сопротивления при движении слева на право	Сила сопротивления при обратном ходе
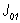
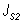
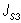
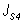
				Pc1	Pc2
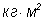
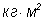
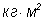
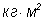
				кН	кН
1,2	0,5	1,2	40	1,5	4,0

Рисунок 2.

2.2. Определение ускорений точек и угловых ускорений звеньев.

Строим план скоростей для заданного положения механизма (mV=0,01 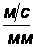). Определяем угловые скорости звеньев.