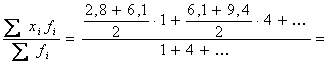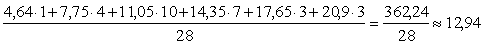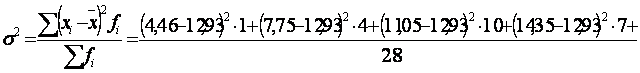Организация финансов на коммерческих предприятиях

Организация финансов на коммерческих предприятиях

стр.

1. Обоснование объема и оценка параметров распределения

выборочной совокупности 4

2. Основные экономические показатели состояния и развития сельскохозяйственного производства 10

2.1. Земельный фонд, его структура и эффективность его

использования 11

2.2. Уровень обеспеченности и эффективности использования

трудовых ресурсов 12

2.3. Материально-техническая база 13

2.4. Специализация исследуемой совокупности 14

2.5. Финансовые результаты деятельности предприятий 14

3. Экономико-статистический анализ производительности труда 16

3.1. Выявление факторов и оценка их влияния на результаты

производства 16

3.2. Расчет нормативов и анализ экономической эффективности

производства на их основе 26

Список использованной литературы 32

Приложения 33

На современном этапе развития экономики большое значение приобретает проблема повышения производительности труда и эффективности использования трудовых ресурсов на предприятиях, так как в условиях рыночных отношений неизбежна сильная конкуренция между фирмами, что толкает их к постоянному повышению качества своей продукции и снижению издержек производства. Это обстоятельство в конечном счете изменяет требования к персоналу в сторону повышения их профессионализма и творческого отношения к труду. Какие бы технические возможности не открывались перед предприятием, оно не будет эффективно работать без квалифицированных специалистов - знатоков своего дела. Грамотно подобранный персонал – залог успеха предприятия.

Для оценки производительности труда, а следовательно и качества трудовых ресурсов, используется экономико-статистический анализ, позволяющий выявить неиспользованные резервы и разработать предложения по повышению эффективности производства. Основные методы экономико-статистического анализа будут изложены в данном курсовом проекте. Объектами анализа послужат сельскохозяйственные предприятия центральной зоны Кировской области.

Целью данного курсового проекта является закрепление теоретических знаний и приобретение практических навыков в обработке статистической информации, а так же применение экономико-статистических методов в анализе.

1. Обоснование объема и оценка параметров распределения выборочной совокупности

Выявление основных свойств и закономерностей исследуемой статистической совокупности начинается с построения ряда распределения единиц по какому-либо группировочному признаку. Группировочный признак – это варьирующий признак по которому производится объединение единиц совокупности в группы. С учетом темы курсового проекта таким признаком была выбрана «выручка на одного работника». Оценив параметры ряда распределения можно сделать вывод о степени однородности, о возможности использования её единиц для проведения экономико-статистического исследования.

Ряд распределения – это группировка единиц совокупности по величине какого-либо варьирующего признака. Ряды распределения могут быть дискретными, если варианты представлены целыми числами, и интервальными, если варианты представлены интервалами. Дискретный ряд строится в том случае, если небольшое число вариантов признака представлено в виде прерывных чисел. Если же признак изменяется непрерывно, то строят интервальный вариационный ряд распределения.

Рассмотрим порядок построения интервального ряда распределения хозяйств центральной зоны Кировской области по выручке на одного работника:

1. Располагаем хозяйства в порядке возрастания выручки на одного работника (тыс. руб.): 2,8; 6.7; 7.3; 8.8; 9.3; 10.4; 10.5; 10.8; 10.9; 11.2; 11.7; 11.8; 11.8; 12.0; 12.1; 13.0; 13.6; 13.8; 13.8; 14.7; 14.8; 15.2; 17.3; 17.9; 18.1; 19.9; 21.1; 22.5

2. Определяем количество интервалов по формуле Стерджесса: k = 1+3,322 lg N

где N – число единиц совокупности

При lg 30 = 1,477

k = 1+ 3,322х1,477 = 5,91 ≈ 6

3. Определяем величину интервала:

h = ,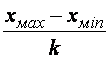

где X max , X min – наибольшее и наименьшее значение группировочного признака, k – количество интервалов

Подставляем значения в формулу и получаем величину интервала равную 2,84 тысячи рублей:

h = 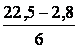≈ 3,3 (тыс. руб.)

4. Определяем границы интервалов.

Для этого X min = 2,8 принимаем за нижнюю границу первого интервала, а его верхняя граница равна: X min + h = 2,8+3,3 = 6,1

Верхняя граница первого интервала одновременно является нижней границей второго интервала. Прибавляя к ней величину интервала (h) определяем верхнюю границу второго интервала: 6,1+3,3=9.4

Аналогично определяем границы остальных интервалов.

5. Подсчитаем число единиц в каждом интервале (см. таблицу 1)

Таблица 1

Интервальный ряд распределения хозяйств по выручке на одного работника

Для наглядности интервальные ряды распределения представленные в таблице 1 можно изобразить в виде гистограммы (см. график 1):

График 1

Распределение хозяйств по выручке на одного работника

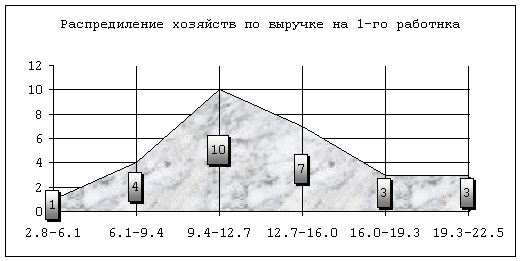
По данным гистограммы можно сделать вывод, что в большинстве хозяйств выручка на одного работника находится в интервале от 9,4 до 12,7 тысяч рублей, а в среднем 11,05 тыс. руб.

Одним из наиболее распространенных законов распределения, с которым сравнивают другие распределения, является нормальное распределение. Для того, чтобы установить верно ли предположение о том, что полученное распределение подчиняется закону нормального распределения, необходимо определить являются ли расхождения между фактическими и теоретическими частотами случайными или закономерными. Для проверки этой статистической гипотезы используeтся критерий, разработанный К. Пирсоном.

Критерий Пирсона определяют по формуле:

Х2факт.= ,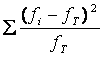

где fi и fТ частоты фактического и теоретического распределения.

Теоретические частоты для каждого интервала определяем в следующей последовательности:

1. Для каждого интервала определяем нормированное отклонение (t) по формуле: t =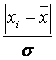

где хi – серединное значение интервала;

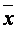- средняя величина признака;

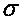- среднее квадратическое отклонение характеризуемого признака в ряду распределения.

Проведем необходимые расчеты параметров исходного ряда распределения:

=
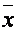