Анализ и синтез систем автоматического регулирования

Страница 2

Для построения областей устойчивости воспользуемся условием, данным в пункте 5 рекомендаций к курсовой работе:

,

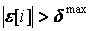где 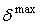- достаточно большая величина на порядок превышающая величину выходной переменной. Принимаем .

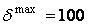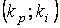
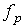
Область устойчивости системы на плоскости коэффициентов регулятора приведена на рис. 4.

Области устойчивости системы на плоскостях 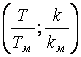, , 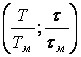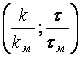приведены на рис. 5, 6 и 7 соответственно.

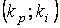
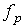
"Неровность" границы областей устойчивости связана с тем, что на интервале моделирования модуль ошибки регулирования расходящегося процесса "не успел" превысить заданную величину. На рис. 8 отображена область устойчивости на плоскости регулятора . Цвет характеризует время переходного процесса (чем ярче точка, тем короче переходный процесс), заштрихованная область – это область, в которой переходный процесс не завершился на интервале моделирования и модуль величины ошибки не превысил максимального значения.

По рис. 8 можно определить направление расширения области (в сторону "гребней"), в которой, при увеличении интервала моделирования, переходный процесс успеет завершится. Во всех остальных областях устойчивости наблюдается аналогичная картина – лучеобразное расширение области при увеличении интервала моделирования (например, рис. 9 – область устойчивости (T/Tм; t/tм)).

5. Исследование чувствительности системы

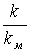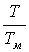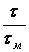Для исследования чувствительности системы варьируются параметры ; ; на интервале ±50% от номинальной величины при единичном задающем воздействии (рис. 10, 11 и 12) и единичном неконтролируемом возмущении (рис. 13, 14 и 15). Показателем чувствительности были выбраны интегральная ошибка системы (сплошная линия) и время регулирования (штрихпунктирная линия).

Вывод

Исследование чувствительности системы показало, что увеличение отношения 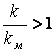при единичном задающем воздействии вызовет резкий скачек времени регулирования, связанный с колебательностью переходного процесса, и незначительно уменьшит интегральную ошибку системы. По этой же причине произойдет скачек времени регулирования при изменении отношения 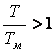и 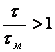, но интегральная ошибка увеличится. Уменьшение данных отношений вызовет плавное увеличение времени регулирования.

При единичном возмущающем воздействии уменьшение отношений (приблизительно на 0.95) вызовет резкий спад времени регулирования и последующее его плавное увеличение. При увеличении отношени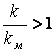й и 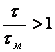будет увеличиваться интегральная ошибка системы и, скачкообразно, время регулирования. Для 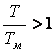время регулирования будет увеличиваться плавно.

В обоих случаях, при вариации коэффициентов, интегральная ошибка системы не изменяется более чем на 45%.

Список литературы

1. Ротач В. Я. Расчет динамики промышленных автоматических систем регулирования. – М.: Энергия, 1973. -440с.

2. Анализ и синтез систем автоматического регулирования: Метод. указ. Сост.: Ю. Н. Марченко: НФИКемГУ. – Новокузнецк, 2001. – 14 с.