Организация статистического контроля качества дорожно-строительных работ
Страница 3
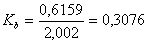
0,3076>0,15 - неоднородная выборка
2.4. Определение абсолютной и относительной погрешностей выборки. Оценка влияния числа измерений на точность определения статистических характеристик.
Вывод: При выборке N=10 среднеарифметическое значение имеет низкую погрешность, остальные значения погрешностей достаточно высоки (более 5%). При выборке N=5 среднеарифметическое значение также имеет низкую погрешность, остальные значения погрешностей высоки (более 50%), а дисперсия более 100%. В целом, можно заключить, что при N=10 меньших процент погрешностей, чем при N=5.
Учитывая вышеизложенное, можно сказать, что с увеличением числа измерений точность определения характеристик возрастает, как следствие, погрешности уменьшаются.
Контрольная карта N = 5
Контрольная карта N = 10
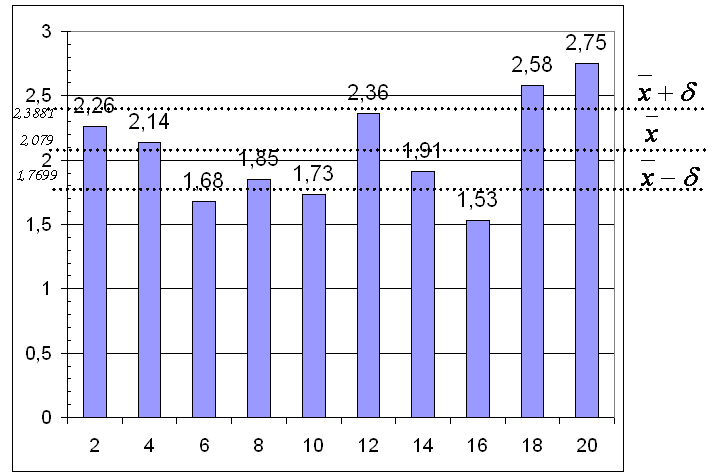Контрольная карта N = 20
3. Интервальная оценка параметров распределения.
1. Определить границы доверительного интервала для единичного результата измерения по формуле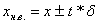 
для N = 20 для всех уровней Pдов.
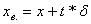
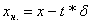
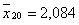
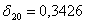
2. Построить кривую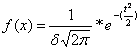 
.
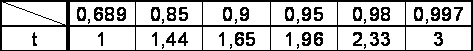
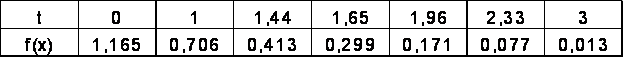
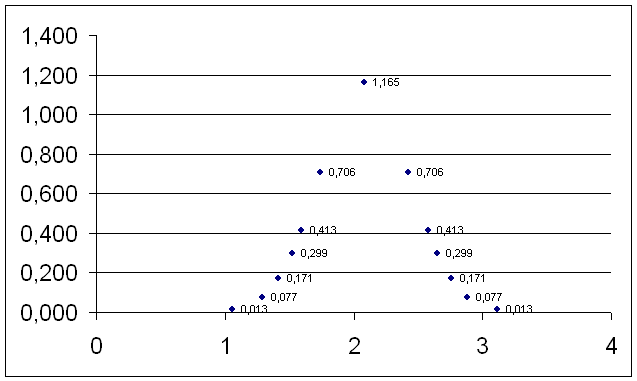
3. Определить границы доверительного интервала для истинного значения
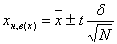для N=20; 10; 5 для всех уровней Pдов.
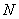
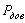
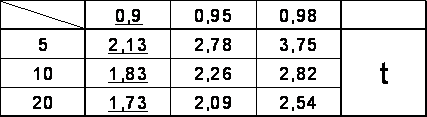
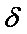
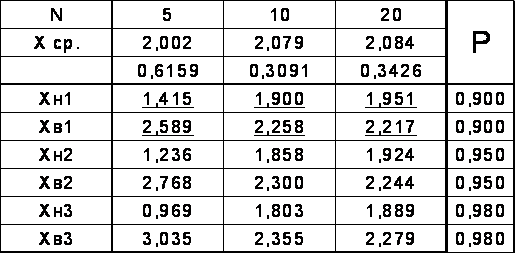
4. Графически изобразить интервалы для N=20; 10; 5 при Pдов. = 0,9
Вывод: С уменьшением количества измерений границы доверительного интервала раздвигаются (для истинного значения случайной величины).
5. Исключение результатов, содержащие грубые погрешности.
Выборку из 20-ти измерений проверить на наличие результатов с погрешностями
методом «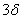
».
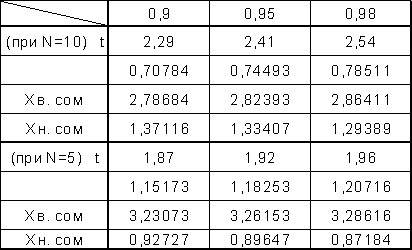
X20=2,084 Xmax = 2,75
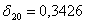Xmin=1,44
t=3
Pдов.=0,997
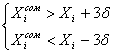
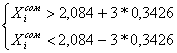
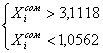
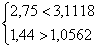
Неравенства являются верными, следовательно, в данной выборке (N=20) нет величин, содержащих грубую погрешность
2. Проверить выборки из 5-ти и 10-ти измерений на наличие результатов в погрешностями по методу Романовского для 3-х уровней доверительной вероятности. Определить при каком уровне доверительной вероятности появляется необходимость корректировать выборку.
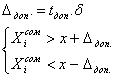Для N=10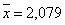 
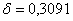
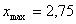
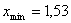
Для N=5 
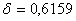
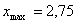
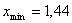
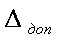
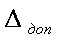
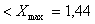
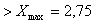
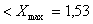
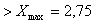
Вывод: в выборках при N=10; 5 нет значений, содержащих грубую погрешность, следовательно нет необходимости в корректировке данных при всех уровнях доверительной вероятности Pдов.
Часть 3
Проверка гипотезы о подчинении выборки нормальному закону распределения.
1. Построение гистограммы экспериментальных данных.
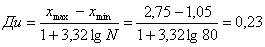
2. Построение теоретической кривой.
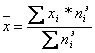
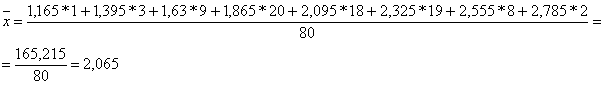
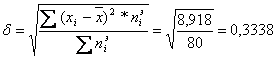
3. Вычисление
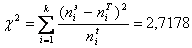
4. Оценка согласия экспериментальных и теоретических данных
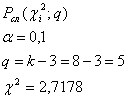
при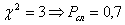 
при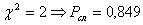
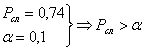
Вывод: Гипотеза не отвергается, т.к. существует большая вероятность того, что расхождение между теоретическими и экспериментальными данными - случайность, обусловленная недостатком числа измерений или недостаточной точностью измерений.
|
Интервал |
Границы интервала |
Середина интервала
|
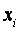
Частота
|
|
|
|
|
|
|
|
|
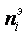
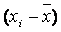
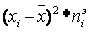
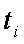
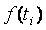
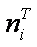
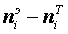
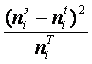
Нижняя |
Верхняя |
|
1 |
1,05 |
1,28 |
1,165 |
1 |
-0,900 |
0,810 |
2,70 |
0,01 |
0,551 |
0,449 |
0,365 |
|
2 |
1,28 |
1,51 |
1,395 |
3 |
-0,670 |
1,347 |
2,01 |
0,051 |
2,811 |
0,189 |
0,013 |
|
3 |
1,51 |
1,75 |
1,63 |
9 |
-0,435 |
1,703 |
1,30 |
0,164 |
9,040 |
-0,040 |
0,000 |
|
4 |
1,75 |
1,98 |
1,865 |
20 |
-0,200 |
0,800 |
0,60 |
0,325 |
17,915 |
2,085 |
0,243 |
|
5 |
1,98 |
2,21 |
2,095 |
18 |
0,030 |
0,016 |
0,09 |
0,393 |
21,663 |
-3,663 |
0,619 |
|
6 |
2,21 |
2,44 |
2,325 |
19 |
0,260 |
1,284 |
0,78 |
0,275 |
15,159 |
3,841 |
0,973 |
|
7 |
2,44 |
2,67 |
2,555 |
8 |
0,490 |
1,921 |
1,47 |
0,116 |
6,394 |
1,606 |
0,403 |
|
8 |
2,67 |
2,9 |
2,785 |
2 |
0,720 |
1,037 |
2,16 |
0,029 |
1,599 |
0,401 |
0,101 |
|
Сумма |
80 |
|
8,918 |
|
2,7178 |
 |
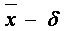1,7312 |
|
1,00 |
0,229 |
12,623 |
|
 |
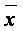2,065 |
|
0,00 |
0,398 |
21,939 |
|
 |
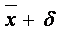2,3988 |
|
1,00 |
0,229 |
12,623 |
|
| | | | | | | | | | | | | | |