Вниз по лестнице температур

Страница 3

А что происходит вне сверхпроводника, при помещении его в магнитное поле? Если сверхпроводник имеет форму узкого цилиндра или узкой пластины, располагающихся вдоль силовых линий приложенного поля, то внесение его в магнитное поле не искажает заметным образом картину силовых линий этого поля.

Если же проводник имеет иную форму, то в его присутствии распределение силовых линий поля существенно изменяется. Например, если образец имеет вид шара, то силовые линии расступаются перед шаром, сгущаются в окрестности его экватора и снова смыкаются позади шара.

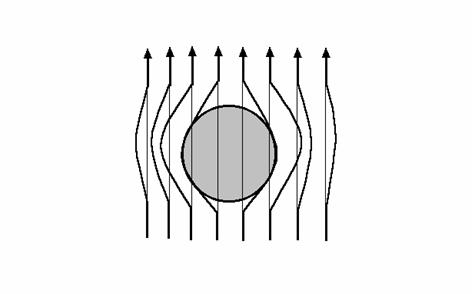
Число силовых линий, пересекающих площадку постоянного сечения, есть мера напряженности поля. Сгущение силовых линий около экватора шара говорит о том, что магнитное поле здесь сильнее, чем вдали от шара.

Пока приложенное к сверхпроводнику магнитное поле невелико, неоднородность этого поля, вызванная образцом, для сверхпроводника несущественна. Но когда поле начинает приближаться к критическому, на проводнике возникают чередующиеся нормальные и сверхпроводящие области. Когда же достигается критическое значение, проводник целиком переходит в нормальное состояние.

А что будет со сверхпроводником, если к нему подключить электрический ток? По мере нарастания тока собственное его поле увеличивается и, наконец, наступает момент, когда оно достигает значения, равного критическому в случае приложения внешнего магнитного поля. Сверхпроводимость исчезает, т.к. сверхпроводнику все равно, какое поле на него действует - собственное поле тока или внешнее магнитное поле. Соответствующее значение тока тоже было названо критическим.

За четверть века, прошедшую с момента открытия сверхпроводимости, были выявлены основные ее черты. Прежде всего выяснилось, что это явление не уникально и присуще целому ряду металлических элементов, причем для всех них температура перехода в сверхпроводящее состояние оказалась очень низкой, порядка нескольких Кельвинов. Затем было установлено, что сверхпроводимость разрушается магнитным полем. В зависимости от формы образца и его ориентировки в магнитном поле это разрушение могло происходить либо скачком по достижении критического поля, либо постепенно по достижении такого поля сначала в отдельных участках образца. Был открыт важнейший эффект Мейснера - Оксенфельда: выталкивание магнитного поля из сверхпроводящих образцов вне зависимости от тех условий, в каких поле прикладывается к образцам. Далее, было обнаружено существование критических токов в сверхпроводниках. И наконец, появилась первая теория сверхпроводимости Лондонов, которая учитывает идеальную электропроводность и идеальный диамагнетизм сверхпроводников.

Новая теория сверхпроводимости

Основной класс веществ, в которых разыгрываются известные эффекты сверхпроводимости, являются металлические кристаллы. Микроскопической теории сверхпроводимости предстояло выяснить, какую роль в этих эффектах играют частицы, из которых состоят кристаллы, - электроны и ионы.

Теория Лондонов не могла объяснить промежуточного состояния. Нужна была новая теория. Волновая функция в сверхпроводящей области отличается от таковой в нормальной области, а на границе между ними достаточно быстро меняется. Кроме того, это не совсем обычная волновая функция: она описывает только коллектив сверхпроводящих электронов. В нормальной области таких электронов нет, и, естественно , волновая функция в ней должна обратиться в нуль. Это обращение в нуль на границе сверхпроводящей и нормальной областей должно произойти постепенно. Чтобы соответствовать тому, что получается на опыте, волновая функция должна постепенно уменьшаться по величине по мере повышения температуры сверхпроводника и обращаться в нуль при критической температуре, когда сверхпроводящие области вовсе исчезают. Для получения необходимых уравнений для волновой функции, нужно было учесть сам переход в сверхпроводящее состояние, т.е. тот факт, что при определенной температуре свободная энергия сверхпроводящей фазы должна стать меньше, чем у нормальной фазы. Следовало принять во внимание также и то, что на сверхпроводимость влияет магнитное поле, создавая чередование нормальных и сверхпроводящих областей и вовсе разрушая сверхпроводимость при достижении критической напряженности во всем образце.

Движение сверхпроводящих электронов более упорядочен, чем движение нормальных электронов. Сущность этого упорядочения пока была непонятна, но само возникновение сверхпроводимости можно было истолковать как фазовый переход от менее к более упорядоченному состоянию. В отсутствии магнитного поля такой переход не сопровождался выделением или поглощением тепла. В таких условиях фазовый переход относится ко второму порядку. Если же переходу характерно скачкообразное изменение среднего расстояния между атомами или молекулами в веществе (при изменении такого расстояния либо затрачивается, либо выделяется энергия), то это фазовый переход первого рода.

Но существуют и такие превращения, при которых средние расстояния между атомами меняются не скачком, а непрерывно, но даже наималейшее изменение расстояний равносильно скачкообразному изменению порядка их взаимного расположения. Порядок расположения атомов в кристалле характеризуется определенной симметрией, и в отличие от расстояния симметрия не непрерывная, а дискретная характеристика: данная симметрия может исчезать или появляться лишь скачком.

Симметрией можно характеризовать не только взаимное расположение атомов в кристалле. Ею можно описывать электрические и магнитные свойства кристаллов и даже движение частиц. Превращения вещества, в которых их состояния меняются непрерывно, а симметрия скачком, были названы фазовыми переходами второго рода.

Симметрия связана со степенью упорядоченности движения частиц. Отличие нового порядка от старого можно описывать, вводя специальную величину - параметр порядка. Понимают, что он равен нулю для старого порядка и возрастает, по мере того как различие нового и старого порядка становится все более значительным.

Роль параметра порядка в своей теории Гинзбург и Ландау уготовили квадрату волновой функции сверхпроводящих электронов. При критической температуре она обращается в нуль. При понижении температуры она возрастает: все большая доля электронов принимает участие в сверхпроводимости, а квадрат волновой функции как раз дает вероятность обнаружить такой электрон. Эта вероятность пропорциональна общему числу электронов.

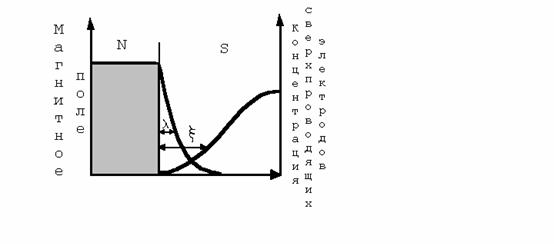
Построим рисунок, изображающий магнитное поле и квадрат волновой функции (концентрацию) сверхпроводящих электронов на границе сверхпроводящей и нормальной областей. Ход магнитного поля характеризуется экспоненциальной зависимостью от расстояния до границы, и мерой быстроты спада магнитного поля является глубина проникновения l. Аналогично изменяется - но в противоположную сторону - квадрат волновой функции; мера быстроты ее изменения получила название длины когерентности: обычно ее обозначают x.

Гинзбург и Ландау выяснили, что поверхностная энергия будет положительной, если отношение l/x меньше, чем 1/Ö2»0,7.

Мы имеем дело с таким сверхпроводником, у которого на границе с нормальными областями концентрация сверхпроводящих электронов снижается до нуля постепенно. Быстрота этого снижения определяется длиной когерентности, и надо рассмотреть две возможности, соответствующие тому, что длина когерентности меньше или больше глубины проникновения.

В первом случае магнитное поле, проникая в сверхпроводник, встречает почти во всей зоне проникновения "полноценный" сверхпроводник с полной концентрацией сверхпроводящих электронов. Поверхностная энергия в этом случае должна быть отрицательной.

Во втором случае почти во всей пограничной области между сверхпроводником и нормальным металлом магнитное поле равно нулю. Приграничная область напоминает сверхпроводник вдали от границы, но концентрация сверхпроводящих электронов в ней все же понижена по сравнению с удаленной от границы областью. Энергия в единице объема приграничной области выше, чем энергия в единице объема области, удаленной от границы, и ближе к энергии в единице объема нормального металла. Тогда энергия, отнесенная к единице площади границы, - это и есть поверхностная энергия, - должна быть положительной.