Возникновение водоворота
Возникновение водоворота
Если налить полную ванну воды, а затем вытащить пробку, то небольшая воронка возникнет на исходе вытекания воды. Вода в ванне или в каком-либо ином сосуде с дыркой на дне всегда закручивается в одну сторону. Даже если воду раскрутить рукой в другом направлении, то, преодолев насилие, она вернет свою природную закрутку. Это связано с силой Кориолиса, которая вызвана вращением Земли вокруг своей оси, причем вектор силы изменяется с широтой. В северном полушарии вода закручивается по часовой стрелке, в южном - против, на экваторе - сливается без вихрей, а на полюсах совсем не течет. Сила Кориолиса является силой инерции. Эта сила действует на тело только тогда, когда неинерциальная система отсчета вращается, а тело движется относительно нее.
Kориолисова сила инерции:
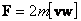 , где m - масса тела, v - скорость поступательного движения,
, где m - масса тела, v - скорость поступательного движения,
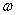 - скорость вращательного движения тела.
- скорость вращательного движения тела.
Рассчитаем силу Кориолиса, действующую на человека массой m=60 кг, движущегося со скоростью v=1 м/c, находящегося на географической широте 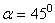 :
:
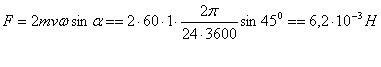 .
.
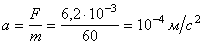 .
.
Кориолисово ускорение на нашей широте очень мало, поэтому мы его не ощущаем. Но с силой Кориолиса связаны такие природные явления, как подмытие правых берегов рек, движущихся в меридиональном направлении, или возникновение смерчей и т.д.
Принцип измерения сил Кориолиса
 В качестве датчика используется U-образная трубка, помещенная в электромагнитное поле регулируемой частоты. Под действием этого поля трубка колеблется, причем амплитуда колебаний будет наибольшей на частоте резонанса (рис. 1, а).
В качестве датчика используется U-образная трубка, помещенная в электромагнитное поле регулируемой частоты. Под действием этого поля трубка колеблется, причем амплитуда колебаний будет наибольшей на частоте резонанса (рис. 1, а).
|
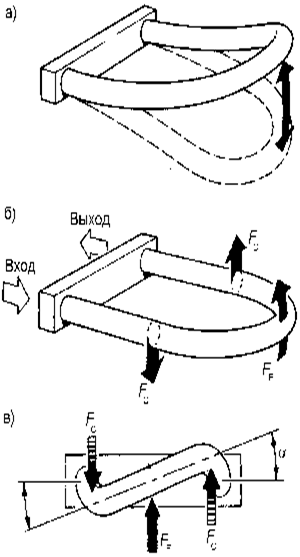
Рис. 1. Принцип измерения, построенный на определении силы Кориолиса (FC):
а - колебания трубки; б - возникновение сил Кориолиса; в - поворот трубки ; FE - сила э.м. поля; 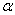 - угол поворота . - угол поворота . | |
Изменение массы вызывает изменение резонансной частоты. Это изменение частоты измеряют и оценивают, на базе чего определяют изменение массы. Поскольку геометрические размеры трубки не меняются, то изменения резонансной частоты определяются массой протекающей через трубку жидкости. Мгновенное значение объема заполняющей трубку жидкости постоянно и определяется неизменными размерами трубки, поэтому изменение резонансной частоты может определяться только плотностью протекающей жидкости.
Жидкость, протекающая в трубке, взаимодействует с импульсами колебаний последней (рис. 1, б). Если, например, трубка движется вверх, то протекающая в ней жидкость давит на нее вниз, замедляя движение трубки. Одновременно жидкость получает от трубки импульс, направленный вверх. На выходе из трубки этот импульс действует таким образом, что движение петли в этом месте усиливается. В то же время на входе движение трубки тормозится, в результате чего образуется момент вращения, стремящийся повернуть датчик (рис. 1, в). Если трубка движется вниз, то момент ее вращения будет направлен в другую сторону. Это явление называется эффектом Кориолиса.
Угол поворота датчика пропорционален массе протекающей жидкости и служит ее мерой. При отсутствии потока угол поворота равен нулю. Когда плотность и масса протекающей жидкости определены, можно делать вывод о ее объеме.
На базе высокой технологии изготовления датчика и современной электронной системы обработки результатов измерений промышленность выпускает приборы, диапазон измерений которых оценивается соотношением 1:200 (обычные системы имеют диапазон измерения 1:10). Точность измерения новых приборов составляет 0,1 %, обычных 0,3 %.
Движение воды в водовороте.
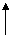
 Пусть в воде находится тело, таких размеров, что его взаимодействием с молекулами воды можно пренебречь. Тело совершает вращательное движение вокруг центра О на расстоянии R1 от него со скоростью
Пусть в воде находится тело, таких размеров, что его взаимодействием с молекулами воды можно пренебречь. Тело совершает вращательное движение вокруг центра О на расстоянии R1 от него со скоростью 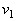 . R2 v1
. R2 v1
 Момент импульса этого тела
Момент импульса этого тела
 L равен:
L равен:


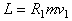 . O m
. O m
Представим теперь, что это тело вращается
вокруг центра О на расстоянии R2<R1 R1
со скоростью 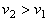 , тогда:
, тогда:
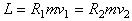 .
.
Выразим отсюда величину 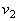 :
:
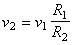 , т.е. приближение к центру вращения приводит к увеличению скорости тела.
, т.е. приближение к центру вращения приводит к увеличению скорости тела.
Напишем выражения для угловых скоростей: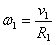 ,
,
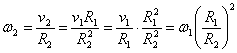 .
.
Отсюда следует, что угловая скорость возрастает обратно пропорционально квадрату радиуса, то есть увеличение частоты вращения может быть очень большим.
Сравним кинетическую энергию тел, находящихся на расстояниях R1 и R2 от центра О:
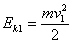 ,
,
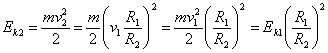 .
.
Ускорение вращения связано с таким же увеличением кинетической энергии тела. Это возможно благодаря тому, что потенциальная энергия опускающейся воды уменьшается, и по закону сохранения энергии она используется на увеличение кинетической энергии, то есть на увеличение скорости движения.
Турбулентность.
При малых скоростях наблюдается упорядоченное течение жидкости (газа), при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Такое течение называется ламинарным. С увеличением скорости в некоторый момент режим течения меняется, оно становится турбулентным.
Необычность явления заключается в том, что картина течения жидкости изменяется во времени, даже если внешние условия постоянны. Например, в турбулентном течении в трубе при неизменном перепаде давления на концах трубы скорость жидкости в любой точке пульсирует, меняется во времени. При таком течении жидкости или газа отдельные элементы течения совершают неустановившиеся движения по сложным траекториям. В таких течениях образуются многочисленные вихри различных размеров, поэтому скорость частиц, температура, давление, плотность меняются при переходе от точки к точке и во времени не регулярно. Это приводит к интенсивному перемешиванию вещества.
Систематическое изучение турбулентности начал О.Рейнольдс в конце прошлого века. Он изучал течение жидкости в трубе, для визуализации течения он подкрашивал жидкость в центре сечения трубы. При малом перепаде давления подкрашенная струйка жидкости не смешиваясь с остальной жидкостью в объеме трубы, спокойно текла вместе с ней. При некотором критическом перепаде давления по подкрашенной струйке появлялись волнообразные движения. При очень большом перепаде давления скорость движения внутри трубы было быстрым и хаотичным, струйка сразу же размешивалась по трубе. Рейнольдс проводил опыты с разными размерами труб и жидкостями и выяснил, что переход от стационарного течения жидкости к меняющемуся во времени происходит, когда некоторая безразмерная комбинация скорости жидкости, ее вязкости и размеров трубы достигает одного и того же значения. Эта безразмерная комбинация имеет вид: