Волновая оптика

Страница 2

Учёт амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т.е. определить закономерности распространения света.

Дифракция Френеля на круглом отверстии:

Сферическая волна, распространяющаяся из точечного источника S, встречает на своём пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром отверстия. Экран параллелен плоскости отверстия и находится от него на расстоянии b. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Для точки В, согласно методу зон Френеля, амплитуда результирующего колебания A=A1/2±Am/2, где знак плюс соответствует нечётным т и минус – чётным т.

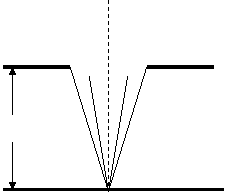
Когда отверстие открывает нечётное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны, если чётное, то амплитуда (интенсивность) будет равна нулю. Если в отверстие укладывается одна зона Френеля, то в точке В амплитуда A=A1, т.е. вдвое больше, чем в отсутствии непрозрачного экрана с отверстием (интенсивность света больше соответственно в четыре раза). Если в отверстие укладывается две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся тёмных и светлых колец с центрами в точке В (если т чётное, то в центре будет тёмное кольцо, если т нечётное – светлое кольцо), причём интенсивность максимумов убывает с расстоянием от центра картины.

Расчёт амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены (число зон Френеля, укладывающихся в отверстии, зависит от λ).

Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своём пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска. В данном случае закрытый диском участок фронта волны надо исключить из рассмотрения и зоны Френеля строить начиная с краёв диска.

Пусть диск закрывает т первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

A=Am+1 – Am+2 + Am+3 -…= Am+1 /2+(Am+1 /2 – Am+2 +Am+3 /2)+…, или A=Am+1 /2, так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружён концентрическими с ним тёмными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины.

Задача. Два груза D и E массами тD =0,25 кг и тЕ =3 кг лежат на гладкой плоскости, наклонной под углом α=30° к горизонту, опираясь на пружину, коэффициент жёсткости которой с=6 Н/см =600 Н/м.

В некоторый момент груз Е убирают; одновременно (t=0) нижний конец пружины В начинает совершать вдоль наклонной плоскости движение по закону ξ =0,02sin 10t (м). Найти уравнение движения груза D.

Решение. Применим к решению задачи дифференциальные уравнения движения точки. Совместим начало координатной системы с положением покоя груза D, соответствующим статической деформации пружины, при условии, что точка В занимает своё среднее положение (ξ=0).

Направим ось x вверх вдоль наклонной плоскости (в сторону движения груза D после снятия груза Е). Движение груза D определяется по следующему дифференциальному уравнению: mD x=∑Xi,

где ∑Xi – сумма проекций на ось х сил, действующих на груз D (рис. а): GD – веса, N – нормальной реакции наклонной плоскости, Р – силы упругости пружины.

Таким образом, mD x = -GD sin α – P.

Здесь P = c(x – fст D – ξ), где fст D – статическая деформация пружины под действием груза D; ξ – перемещение точки прикрепления нижнего конца пружины, происходящее по закону ξ =d sin pt (d =0,02 м, p=10 рад/с).

Статическая деформация пружины fст D найдём из уравнения, соответствующего состоянию покоя груза D на наклонной плоскости (рис. б):

∑Xi =0;

-GD sin α +P0 =0,

т. е. –GD sin α + cfст D =0,

откуда fст D =GD sin α/c.

Дифференциальное уравнение движения груза D имеет вид

mD x = -GD sin α – c(x – fст D – ξ),

или после преобразования mD x + cx = cd sin pt.

Разделив все члены уравнения на mD и введя обозначения

c/mD = k2, cd/mD = h,

приведём дифференциальное уравнение к следующему виду:

x + k2x = h sin pt.

Решение этого неоднородного уравнения складывается из общего решения х*, соответствующего однородного уравнения и частного решения х** данного неоднородного уравнения:

x = x*+ x**.

Общее решение однородного уравнения имеет вид

x* = C1 cos kt +C2 sin kt.

Частное решение неоднородного уравнения:

x** = [ h /(k2 – p2)] sin pt.

Общий интеграл

x = C1 cos kt +C2 sin kt + [ h /(k2 – p2)] sin pt.

Для определения постоянных интегрирования С1 и С2 найдём, кроме того, уравнение для х

x = -C1 k sin kt +C2 k cos kt + [ hp/(k2 – p2)] cos pt

и используем начальные условия задачи.

Рассматриваемое движение начинается в момент (t=0), когда деформация пружины является статической деформацией под действием грузов D и E. При принятом положении начала отсчёта О начальная координата груза D равна x0 = -fст E, причём fст E = GE sin α/c – статическая деформация пружины под действием груза Е.

Таким образом, при t=0

x0 = -fст E, x0 = 0.

Составим уравнение x = x(t) и x = x(t) для t=0:

x0 = C1; x0 = C2 k + hp/( k2 – p2),

откуда

C1 = -fст E, C2 = -hp/[ k( k2 – p2)].

Уравнение движения груза D имеет следующий вид:

x = -fст E cos kt – hp/[ k( k2 – p2)] sin kt + h/( k2 – p2) sin pt.

Найдём числовое значение входящих в уравнение величин:

k =√с/mD = √6 ∙100 /0,25 = 49 c-1;

fст E = GE sin α/c = 3 ∙9,81∙0,5 /6 ∙100 = 0,0245 м.

h/( k2 – p2) = cd/mD( k2 – p2) = 600 ∙0,02/0,25(2400 – 100) = 0,021 м;

hp/ k( k2 – p2) = 0,021 ∙10 /49 = 0,0043 м.

Следовательно, уравнение движения груза D

x = -2,45 cos 49t – 0,43 sin 49t +2,1 sin 10t (см).

Курсовая работа

по

теоретическоймеханике

на тему:

Световыеколебания

Выполнил: студент гр. ПСТ Башев А.Н.

Проверил: к.т.н. Краснов В.Г.

Нижневартовск 2000.