Газы и тепловые машины
Страница 3
На третьей стадии цикла происходит изотермическое и обратимое сжатие газа по пути cd, здесь газ контактирует с холодным термостатом при температуре ТL. И наконец газ адиабатически и обратимо сжимается по пути da возвращаясь, таким образом, в исходное состояние.
Несложно показать, что результирующая работа численно равна площади ограниченной кривыми.
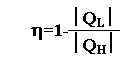КПД двигателя Карно определяется также как и любого другого двигателя:
Однако можно показать, что его КПД зависит лишь от ТН и ТL.
В первом изотермическом процессе ab совершаемая газом работа равна:
Wab=nRTHln(Vb/Va)
, где n - число молей идеального газа, используемого в качестве рабочего тела. Поскольку внутренняя энергия идеального газа не меняется, когда температура постоянна, сообщаемая газу теплота полностью переходит в работу ( в соответствии с первым началом термодинамики):
½QH½=nRTHln(Vb/Va)
Аналогично запишется теплота отдаваемая газом в процессе cd:
½QL½=nRTLln(VC/Vd)
Поскольку bc и da адиабатические процессы, получаем:
PbVb=PcVc и PdVd=PaVa
В соответствии с уравнением состояния идеального газа получаем:
С помощью несложных математических преобразований этих выражений получаем математическое выражение отображающее суть цикла Карно:
Таким образом КПД двигателя Карно можно записать в виде:
|
h=1-½QL½/½QH½=1- TL/TH |
(8) |
Карно сформулировал следующую теорему (являющуюся ещё одной формулировкой второго начала термодинамики):
Все обратимые двигатели, работающие между двумя термостатами, имеют один и тот же КПД; ни один необратимый двигатель, работающий междц теми же термостатами, не может иметь более высокого КПД.
Эта теорема определяет максиммально возможный КПД для любого необратимого (реального) двигателя.
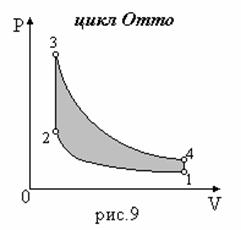Рассмотрим идеальный цикл используемый в двигателях внутреннего сгорания, так называемый цикл Отто (рис. 9).
В этом цикле сжатие и расширение смеси происходит адиабатически, а нагревание и охлаждение осуществляется при постоянном объеме. На рисунке 9 дана диаграмма идеального цикла быстрого сгорания: 1-2 – адиабата сжатия, 2-3 -нагревание смеси при V=const (сгорание смеси), 3-4 адиабата расширения, 4-1 – охлаждение смеси при V=const (выхлоп).
КПД идеального двигателя построенного на основе цикла Отто рассчитывается аналогично. Однако, в реальных двигателях КПД всегда несколько ниже, чем КПД идеального двигателя. Этому способствуют 5 основных причин:
1. В действительном цикле рабочее тело из меняет свой химический состав в течение процесса сгорания.
2. Процессы сжатия и расширения не идут адиабатически, а протекают, сопровождаясь теплообменом со стенками цилиндра. Явление теплообмена со стенками цилиндра имеет место также и в процессе сгорания.
3. Процесс сгорания не происходит при постоянном объеме, а начинается в точке 2’ (рис. 10) и кончается после точки 3. В процессе сгорания тепло получается не извне, а за счет изменения химического состава рабочего тела. Химическая реакция сгорания не успевает закончиться полностью на линии сгорания (2-3), а продолжается в течение процесса расширения вплоть до момента выхлопа.
4. 
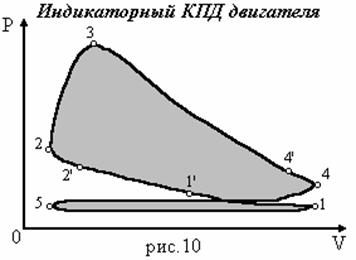Процесс охлаждения рабочего тела в действительности заменяется выхлопом и выталкиванием отработанных газов и последующим засасыванием рабочей смеси (линия 4’-4-5-1).
5. Процесс всасывания заканчивается позднее точки 1 (в точке 1’) так, что от точки 4’ до 1’ в цилиндре находится не постоянное количество рабочего тела.
КПД тепловых двигателей и второе начало термодинамики.
КПД тепловой машины определяется следующей формулой:
, где W - полезная работа совершенная этой машиной, QH - теплота сообщенная этой машине (Q взято под знак модуля, в связи с тем, что тепловой поток может иметь разное направление).
По закону сохранения энергии получаем соотношение:
½QH½=W+½QL½
, где ½QL½ - количество теплоты отводимой при низкой температуре.
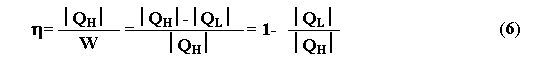Таким образом, W=½QH½-½QL½, и КПД двигателя можно записать в виде:
Из этого соотношения видно, что чем больше будет КПД двигателя, тем меньше будет теплота½QL½. Однако опыт показал, что величину ½QL½ невозможно уменьшить до нуля. Если бы это было осуществимо, то мы получили бы двигатель с КПД 100%. То, что такой идеальный двигатель, непрерывно совершающий рабочие циклы, невозможен, составляет содержание ещё одной формулировки второго начала термодинамики:
Невозможен такой процесс, единственным результатом, которого было бы преобразование отобранной у источника теплоты Q, при неизменной температуре, полностью в работу W, так, что W=Q.
Эта утверждение известно как формулировка второго начала термодинамики Кельвина-Планка.
Существует также аналогичное утверждение относительно холодильника, высказанное Клаузисом:
Невозможно осуществить периодический процесс, единственным результатом, которого был бы отбор теплоты у одной системы при данной температуре и передача в точности такого же количества теплоты другой системе при более высокой температуре.
Уравнение Ван-дер-Ваальса.
В реальных тепловых двигателях используются реальные газы. Как было замечено поведение их заметно отклоняется, например, при высоком давлении, от поведения идеального газа. Ян Д. Ван-дер-Ваальс (1837-1923) исследовал эту проблему с точки зрения МКТ и в 1873 году получил уравнение более точно описывающее поведение реальных газов. Свой анализ он основывал на МКТ, но при этом учитывал:
A. Все молекулы имеют конечные размеры (классическая МКТ ими пренебрегает)
B. Молекулы взаимодействуют друг с другом всё время, а не только во время столкновений.
Предположим, что молекулы газа представляют собой шарики с радиусом r. Если считать, что такие молекулы ведут себя подобно твердым сферам, то две молекулы будут сталкиваться и разлетаться в разные стороны при расстоянии между центрами равным 2r. Таким образом, реальный объем, в котором могут двигаться молекулы несколько меньше, чем объем V сосуда содержащего газ. Величина этого "недоступного объема" зависит от объема молекул газа и от количества этих молекул. Пусть b представляет собой "недоступный объем" в расчете на один моль газа. Тогда в уравнении состояния идеального газа нужно заменить V на V-nb, где n - число молей газа, и мы получим:
P(V-nb)=nRT
Если разделить это выражение на n и считать, что величина v==V/n является объемом, который занят одним молем газа (v - удельный объем), то получим:
Это соотношение показывает, что при данной температуре давление
P=RT/(v-b)
будет больше, чем в идеальном газе. Это происходит потому, что уменьшение объема означает, что число столкновений со стенками возрастает.