Газы и тепловые машины
Газы и тепловые машины
План:
1. Закон идеального газа.
2. Первое начало термодинамики. Адиабатический процесс.
3. Второе начало термодинамики.
4. Принцип действия тепловых машин.
5. КПД тепловых двигателей и второе начало термодинамики.
6. Уравнение Ван-дер-Ваальса.
Закон идеального газа.
Экспериментальный:
Основными параметрами газа являются температура, давление и объём. Объем газа существенно зависит от давления и температуры газа. Поэтому необходимо найти соотношение между объемом, давлением и температурой газа. Такое соотношение называется уравнением состояния.
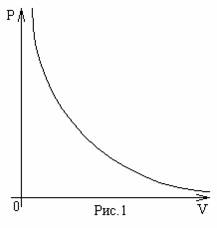
Экспериментально было обнаружено, что для данного количества газа в хорошем приближении выполняется соотношение: при постоянной температуре объем газа обратно пропорционален приложенному к нему давлению (рис.1):
V~1/P , при T=const.
Например, если давление, действующее на газ, увеличится вдвое, то объем уменьшится до половины первоначального. Это соотношение известно как закон Бойля (1627-1691)-Мариотта(1620-1684), его можно записать и так:
PV=const.
Это означает, что при изменении одной из величин, другая также изменится, причем так, что их произведение останется постоянным.
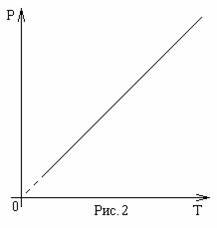
Зависимость объема от температуры (рис.2) была открыта Ж. Гей-Люссаком. Он обнаружил, что при постоянном давлении объем данного количества газа прямо пропорционален температуре:
V~T , при Р=const.
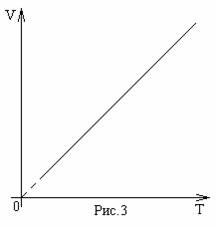График этой зависимости проходит через начало координат и, соответственно, при 0К его объём станет равный нулю, что очевидно не имеет физического смысла. Это привело к предположению, что -2730С минимальная температура, которую можно достичь.
Третий газовый закон, известный как закон Шарля, названный в честь Жака Шарля (1746-1823). Этот закон гласит: при постоянном объеме давление газа прямо пропорционально абсолютной температуре (рис.3):
Р~T, при V=const.
Хорошо известным примером действия этого закона является баллончик аэрозоля, который взрывается в костре. Это происходит из-за резкого повышения температуры при постоянном объеме.
Эти три закона являются экспериментальными, хорошо выполняющимися в реальных газах только до тех пор, пока давление и плотность не очень велики, а температура не слишком близка к температуре конденсации газа, поэтому слово "закон" не очень подходит к этим свойствам газов, но оно стало общепринятым.
Газовые законы Бойля-Мариотта, Шарля и Гей-Люссака можно объеденить в одно более общее соотношение между объёмом, давлением и температурой, которое справедливо для определенного количества газа:
PV~T
Это показывает, что при изменении одной из величин P, V или Т, изменятся и две другие величины. Это выражение переходит в эти три закона, при принятии одной величины постоянной.
Теперь следует учесть ещё одну величину, которую до сих пор мы считали постоянной - количество этого газа. Экспериментально подтверждено, что: при постоянных температуре и давлении замкнутый объём газа увеличивается прямо пропорционально массе этого газа:
PV~mT
Эта зависимость связывает все основные величины газа. Если ввести в эту пропорциональность коэффициент пропорциональности, то мы получим равенство. Однако опыты показывают, что в разных газах этот коэффициент разный, поэтому вместо массы m вводят количество вещества n (число молей).
В результате получаем:
, где n - число молей, а R - коэффициент пропорциональности. Величина R называется универсальной газовой постоянной. На сегодняшний день самое точное значение этой величины равно:
R=8,31441 ± 0,00026 Дж/Моль
Равенство (1) называют уравнением состояния идеального газа или законом идеального газа.
Число Авогадро; закон идеального газа на молекулярном уровне:
То, что постоянная R имеет одно и то же значение для всех газов, представляет собой великолепное отражение простоты природы. Это впервые, хотя и в несколько другой форме, осознал итальянец Амедео Авогадро (1776-1856). Он опытным путём установил, что равные объёмы объемы газа при одинаковых давлении и температуре содержат одинаковое число молекул. Во-первых: из уравнения (1) видно, что если различные газы содержат равное число молей, имеют одинаковые давления и температуры, то при условии постоянного R они занимают равные объёмы. Во-вторых: число молекул в одном моле для всех газов одинаково, что непосредственно следует из определения моля. Поэтому мы можем утверждать, что величина R постоянна для всех газов.
Число молекул в одном моле называется числом Авогадро NA. В настоящее время установлено, что число Авогадро равно:
NA=(6,022045±0,000031)·10-23 моль-1
Поскольку общее число молекул N газа равно числу молекул в одном моле, умноженному на число молей (N=nNA), закон идеального газа можно переписать следующим образом:
PV=nRT=N/NART
или
, где k называется постоянной Больцмана и имеет значение равное:
k= R/NA=(1,380662±0,000044) ·10-23 Дж/К
Первое начало термодинамики. Адиабатический процесс.
Внутренняя энергия газа - это сумма кинетической и потенциальной энергии всех молекул этого газа. Очевидно, что внутренняя энергия газа должна увеличиваться либо за счет совершения над газом работы, либо путем сообщения ему некоторого количества теплоты. И наоборот, если газ совершает работу над внешними телами или тепловой поток направлен из газовой системы, то энергия этой системы должна уменьшаться.
В результате опытов Джоуля (как и многих других) был сформулирован закон, согласно которому изменение внутренней энергии (DU) замкнутой системы можно записать в следующем виде:
, где Q-количество теплоты, сообщенное системе, а W-работа совершаемая системой.
Выражение (3) известно как первое начало термодинамики. Поскольку теплота Q и работа W выражают способы передачи энергии в систему или из неё, внутренняя энергия изменяется в соответствии с ними. Таким образом первое начало термодинамики является попросту формулировкой закона сохранения энергии.
Уравнение (3) применимо как к замкнутым системам, так и к не замкнутым, если учесть изменение энергии вследствие изменения количества вещества в данной системе.
При переходе системы из одного состояния в другое (1 в 2) количество теплоты Q, сообщённое системе, и работа W, совершённая системой, зависят от конкретного процесса (или пути), в котором участвовала система. И для разных процессов эти величины различны, даже если начальные и конечные состояния системы одинаковы. Однако эксперименты показали, что при одинаковых начальном и конечном состояниях разность Q-W одинакова для всех процессов, переводящих систему из одного состояния в другое.
Адиабатическим называется процесс, при котором от системы не отбирается и не сообщается энергии. Такой процесс может происходить, если система изолирована или протекает столь быстро, что теплообмен практически не происходит. Примером процесса, очень близкого к адиабатическому, является расширение газов в двигателях внутреннего сгорания.
При медленном адиабатическом расширении из уравнения (3) следует (так как Q=0 (по определению адиабатического процесса)):