Анализ экономических задач симплексным методом
Страница 2
Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называют опорным решением (планом).
Теорема. Если система векторов 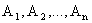 содержит m линейно независимых векторов
содержит m линейно независимых векторов 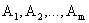 , то допустимый план
, то допустимый план 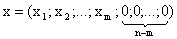 (10) является крайней точкой многогранника планов.
(10) является крайней точкой многогранника планов.
Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.
§2.Графический способ решения ЗЛП.
Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.
Пусть дана задача
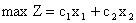 (11)
(11)
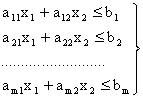 (12)
(12)
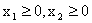 (13)
(13)
Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений (12), (13) задает на плоскости 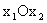 некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
некоторую полуплоскость. Полуплоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (11) — (13) есть выпуклое множество.
Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — непустое множество, например многоугольник 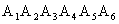 .
.
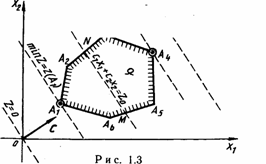
Выберем произвольное значение целевой функции 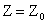 . Получим
. Получим 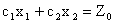 . Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение
. Это уравнение прямой линии. В точках прямой NМ целевая функция сохраняет одно и то же постоянное значение 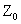 . Считая в равенстве (11)
. Считая в равенстве (11) 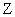 параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).
Найдём частные производные целевой функции по 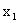 и
и 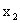
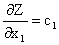 (14)
(14)
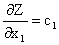 (15)
(15)
Частная производная (14) ((15)) функции показывает скорость ее возрастания вдоль данной оси. Следовательно, 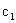 и
и 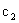 — скорости возрастания
— скорости возрастания 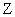 соответственно вдоль осей
соответственно вдоль осей 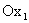 и
и 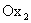 . Вектор
. Вектор 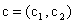 называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
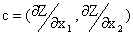
Вектор —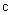 указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
указывает направление наискорейшего убывания целевой функции. Его называют антиградиентом.
Вектор 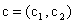 перпендикулярен к прямым
перпендикулярен к прямым 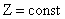 семейства
семейства 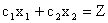
Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок ее графического решения.
1. С учетом системы ограничений строим область допустимых решений 
2. Строим вектор 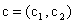 наискорейшего возрастания целевой функции — вектор градиентного направления.
наискорейшего возрастания целевой функции — вектор градиентного направления.
3. Проводим произвольную линию уровня 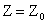
4. При решении задачи на максимум перемещаем линию уровня 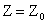 в направлении вектора
в направлении вектора 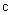 так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня
так, чтобы она касалась области допустимых решений в ее крайнем положении (крайней точке). В случае решения задачи на минимум линию уровня 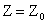 перемещают в антиградиентном направлении
перемещают в антиградиентном направлении
5. Определяем оптимальный план 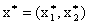 и экстремальное значение целевой функции
и экстремальное значение целевой функции 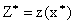 .
.
§3.Симплексный метод.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Пусть ЗЛП представлена системой ограничений в каноническом виде:
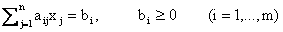 .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части 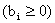 левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
Пусть система ограничений имеет вид
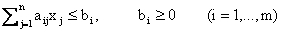
Сведем задачу к каноническому виду. Для этого прибавим к левым частям неравенств дополнительные переменные 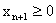
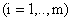 . Получим систему, эквивалентную исходной:
. Получим систему, эквивалентную исходной:
 ,
,
которая имеет предпочтительный вид
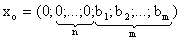 .
.
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю 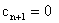
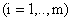 .
.
Пусть далее система ограничений имеет вид
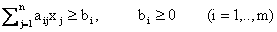
Сведём её к эквивалентной вычитанием дополнительных переменных 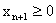
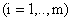 из левых частей неравенств системы. Получим систему
из левых частей неравенств системы. Получим систему

Однако теперь система ограничений не имеет предпочтительного вида, так как дополнительные переменные 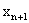 входят в левую часть (при
входят в левую часть (при 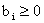 ) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план
) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план 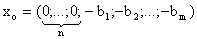 не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные 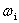 . В целевую функцию переменные
. В целевую функцию переменные 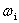 , вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
, вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.