Анализ экономических задач симплексным методом
Страница 4
Теорема. (малая теорема двойственности)
Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
§5. Основные теоремы двойственности
и их экономическое содержание
Теорема.
Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: 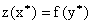 . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
Теорема. (о дополняющей нежесткости )
Для того, чтобы планы 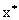 и
и 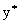 пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий:
пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий:
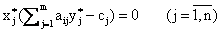 (1)
(1)
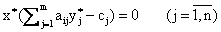 (2)
(2)
Условия (1), (2) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Экономически это означает, что если по некоторому оптимальному плану 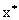 производства расход i -го ресурса строго меньше его запаса
производства расход i -го ресурса строго меньше его запаса 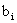 , то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.
, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.
Теорема .(об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее
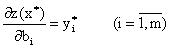 (3)
(3)
§6. Примеры экономических задач
5.1 Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, объединение и т. д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов, может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексом j  . Ее будем обозначать
. Ее будем обозначать 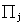 . Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами
. Предприятие при производстве этих видов продукции должно ограничиваться имеющимися видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т. д.). Все эти виды ограничивающих факторов называют ингредиентами  . Пусть их число равно m; припишем им индекс i
. Пусть их число равно m; припишем им индекс i 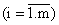 . Они ограничены, и их количества равны соответственно
. Они ограничены, и их количества равны соответственно 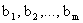 условных единиц. Таким образом,
условных единиц. Таким образом,  - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации
- вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчисляемая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т. д. Примем в качестве такой меры, например, цену реализации
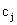
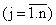 , т. е.
, т. е. 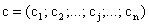 —вектор цен. Известны также технологические коэффициенты
—вектор цен. Известны также технологические коэффициенты 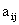 , которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов
, которые указывают, сколько единиц i–го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов 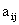 называют технологической и обозначают буквой А. Имеем
называют технологической и обозначают буквой А. Имеем 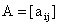 . Обозначим через
. Обозначим через 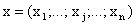 план производства, показывающий, какие виды товаров
план производства, показывающий, какие виды товаров 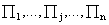 нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
Так как 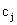 - цена реализации единицы j'-й продукции, цена реализованных
- цена реализации единицы j'-й продукции, цена реализованных 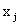 единиц будет равна
единиц будет равна 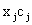 , а общий объем реализации
, а общий объем реализации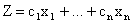
Это выражение — целевая функция, которую нужно максимизировать.
Так как 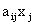 - расход i-го ресурса на производство
- расход i-го ресурса на производство 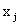 единиц j-й продукции, то, просуммировав расход i-го ресурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить
единиц j-й продукции, то, просуммировав расход i-го ресурса на выпуск всех n видов продукции, получим общий расход этого ресурса, который не должен превосходить 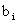
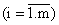 единиц:
единиц:
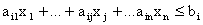
Чтобы искомый план 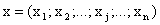 был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы
был реализован, наряду с ограничениями на ресурсы нужно наложить условие неотрицательности на объёмы 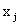 выпуска продукции:
выпуска продукции:
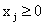
 .
.
Таким образом, модель задачи о наилучшем использовании ресурсов примет вид:
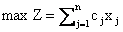 (1)
(1)
при ограничениях:
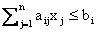
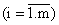 (2)
(2)
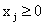
 (3)
(3)