Анализ экономических задач симплексным методом
Страница 6
|
Номера ит. |
БП |
Сб |
|
|
|
|
|
|
|
|
|
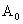
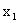
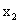
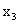
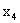
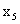
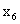
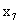
65 |
70 |
60 |
120 |
0 |
0 |
0 |
|
0 |
|
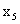
0 |
4800 |
4 |
2 |
2 |
8 |
1 |
0 |
0 |
|
|
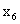
0 |
2400 |
2 |
10 |
6 |
0 |
0 |
1 |
0 |
|
|
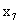
0 |
1500 |
1 |
0 |
2 |
1 |
0 |
0 |
1 |
|
|
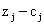
0 |
-65 |
-70 |
-60 |
-120 |
0 |
0 |
0 |
|
1 |
|
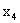
120 |
600 |
1/2 |
1/4 |
1/4 |
1 |
1/8 |
0 |
0 |
|
|
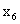
0 |
2400 |
2 |
0 |
6 |
0 |
0 |
1 |
0 |
|
|
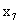
0 |
900 |
1/2 |
-1/4 |
7/4 |
0 |
-1/8 |
0 |
1 |
|
|
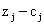
72000 |
-5 |
-40 |
-30 |
0 |
15 |
0 |
0 |
|
2 |
|
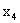
120 |
500 |
5/12 |
-1/6 |
0 |
1 |
1/8 |
-1/24 |
0 |
|
|
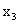
60 |
400 |
1/3 |
5/3 |
1 |
0 |
0 |
1/6 |
0 |
|
|
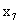
0 |
200 |
-1/12 |
-19,6 |
0 |
0 |
-1/8 |
-7/24 |
1 |
|
|
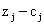
84000 |
5 |
10 |
0 |
0 |
15 |
5 |
0 |
Выпишем из таблицы2. Компоненты оптимального плана двойственной задачи – двойственные оценки. В канонической форме прямой задачи переменные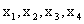 
- являются свободными, а дополнительные переменные 
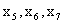- базисными. В канонической форме двойственной задачи свободными будут переменные 
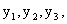- а базисными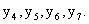 
Соответствие между переменными примет вид
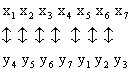
Учитывая это соответствие, выпишем из индексной строки последней итерации компоненты искомого плана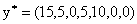 
- двойственные оценки.
min f = max Z =84000.