Задача динамического программирования

Страница 3

N = 3 – число шагов.

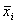- Технологическая линия.

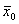
= (0,0,0)

= ( )

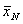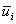– выбор оборудования для i-ой операции.

Ui – область допустимых УВ на i-м шаге.

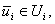т.е.

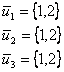
Wi – оценка минимальной себестоимости, полученная в результате реализации i-го шага.

S – функция общего выигрыша т. е. минимальная себестоимость .

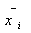
- вектор – функция, описывающая переход системы из состояния в состояние под действием УВ.

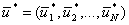- вектор УВ на i-ом шаге, обеспечивающий переход системы из состояния xi-1 в состояние xi , т.е. оптимальный выбор оборудования за N шагов.

Si+1(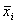) – максимальный выигрыш ( в нашем случае минимальная себестоимость), получаемый при переходе из любого состояния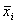 в конечное состояние 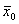при оптимальной стратегии управления начиная с (k+1)-го шага.

S1(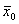) – максимальный выигрыш, получаемый за N шагов при переходе системы из начального состояния 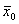в конечное 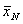при реализации оптимальной стратегии управления 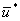. Очевидно, что S = S1(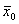), если 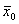= 0.

Запишем вектора допустимых значений

Запишем вектора допустимых управляющих воздействий

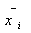
Запишем вектор – функцию, описывающую переход системы из состояния в состояние под действием УВ.

Запишем основное функциональное уравнение

1) Обратный проход

Для i=3

Учитывая то, что этот шаг у нас последний и следующей операции

уже не будет, а также то, что мы на обратном проходе, вместо функции

возьмем стоимость сырья