Изучение состава кадров

Страница 3

2.КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

2.1.Понятие корреляционной связи

Содержание теории корреляции составляет изучение зависимости вариации признака от окружающих условий.

При изучении конкретных зависимостей выявляют факторные и результативные признаки. В корреляционных связях между изменениями факторного и результативного признака нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.

Кроме того, сам признак-фактор в свою очередь может зависеть от изменения ряда обстоятельств. В сложном взаимодействии находится результативный признак – в более общем виде он выступает как фактор изменения других признаков. Отсюда результаты корреляционного анализа имеют значение в данной связи, а интерпретация этих результатов в более общем виде требует построения системы корреляционных связей.

При исследовании корреляционных зависимостей между признаками решению подлежит широкий круг вопросов, к которым следует отнести :

1)Предварительный анализ свойств моделируемой совокупности единиц;

2)Установление факта наличия связи, определение её формы и направления;

3)Измерение степени тесноты связи между признаками;

4)Построение регрессивной модели, т.е. нахождение аналитического выражения связи;

5)Оценка адекватности модели, её экономическая интерпретация и практическое использование.

Для того, чтобы результаты корреляционного анализа нашли практическое применение и дали желаемый результат, должны выполняться определённые требования.

1.Требование однородности тех единиц, которые подвергаются изучению.

2.Количественная оценка однородности исследуемой совокупности по комплексу признаков (расчет относительных показателей вариации, коэффициент вариации, отношение размаха вариации к среднему квадратическому отклонению).

3.Достаточное число наблюдений.

4.Исследуемая совокупность должна иметь нормальное распределение.

5.Факторы должны иметь количественное выражение.

2.2.Статистические методы выявления наличия корреляционной связи между двумя признаками

Простейшим приёмом обнаружения связи является сопоставление двух параллельных рядов – ряда значений признака-фактора и соответствующих ему значений результативного признака. Значение факторного признака располагается в возрастающем порядке и затем прослеживается направление изменения величины результативного признака. Результативный признак (функция) обозначается через y, а факторный признак через x.

Ниже приведён пример обнаружения корреляционной связи между стажем (факторный признак) и заработной платой (результативный признак). В таблице 2.1 работники ранжированы по стажу.

Таблица 2.1.

Сведения о стаже и заработной плате рабочих

на промышленном предприятии

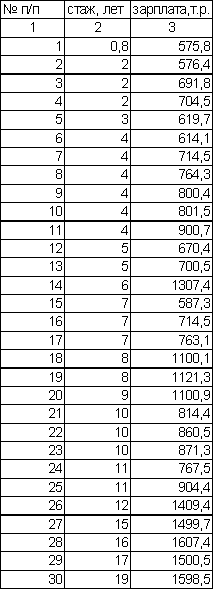
Можно видеть, что в целом для всей совокупности увеличение стажа приводит к увеличению заработной платы, т.е. связь – прямая, хотя в отдельных случаях наличие такой связи не усматривается.

Наличие большого числа различных значений результирующего признака затрудняет восприятие таких параллельных рядов. В таких случаях целесообразнее воспользоваться для установления факта наличия связи корреляционной таблицей. Корреляционная таблица позволяет изложить материал сжато, компактно и наглядно.

Построение корреляционной таблицы начинают с группировки значений фактического и результативного признаков. В первый столбик следует вписать значения факторного признака (x), а первую строку заполнить значениями результативного признака (y). Числа, полученные на пересечении строк и столбцов, означают частоту повторения данного сочетания значений x и y.

Таблица 2.2.

Корреляционная таблица зависимости заработной платы от стажа

Центральные значения	660	830	1170	1340	1515
Группы по х	Группы по у
	До 745	745-915	1085-1255	1255-1425	Свыше 1425	fx	yj
До 5 лет	7	4				11	722
5-8 лет	3	2	2	1		8	915
8-11 лет		3	1			4	915
11-14		2		1		3	1000
14-17					2	2	1515
Свыше17 лет					2	2	1515
fy	10	11	3	2	4	30

Примечание: В таблице используются следующие обозначения:

yj – среднее значение результативного признака для j-той группы значений факторного признака;

fx – частота повторения данного варианта значения факторного признака во всей совокупности;

fy – частота повторения результативного признака во всей совокупности.

Данная корреляционная таблица уже при общем знакомстве даёт возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить её направление, Если частоты расположены по диагонали из верхнего левого угла в правый нижний, то связь между признаками прямая. Если же частоты расположены по диагонали справа налево, - то связь обратная. В данном случае можно предположить наличие прямой связи.