Количественные методы в управлении

Страница 2

Так как все оценочные коэффициенты неотрицательны, то получено оптимальное решение. Оптимальное решение: x1=34, x2=0, x3=24, x4=0, x5=0, x6=20, x7=0. Максимум целевой функции Pmax= 2328.

Ресурсы 1 и 3 являются «узким местом» производства, так как при выполнении оптимального плана они используются полностью (без остатка).

1.2 Двойственная задача линейного программирования.

исходная задача двойственная задача

CX-->max YB-->min

AX<=B, X>=0 YA>=C, Y>=0

P= 48*x1+30*x2+29*x3+10*x4 -->max S= 198*y1+96*y2+228*y3 -->min

3*x1+2*x2+4*x3+3*x4<=198 3*y1+2*y2+6*y3>=48

2*x1+3*x2+1*x3+2*x4<=96 2*y1+3*y2+5*y3>=30

6*x1+5*x2+1*x3+0*x4<=228 4*y1+1*y2+1*y3>=29

x1,x2,x3,x4>=0 3*y1+2*y2+0*y3>=10

y1,y2,y3>=0

Первый способ:

По первой теореме двойственности, оптимальные решения двойственной задачи (y1,y2,y3) равны оценочным коэффициентам при балансовых переменных последней симплекс-таблицы: у1=6, у2=0, у3=5. А экстремум двойственной задачи Smin=2328.

Второй способ:

По второй теореме двойственности, если какая-то компонента оптимального решения исходной задачи отлична от нуля, то соответствующее ей ограничение двойственной задачи на ее оптимальном решении выполняется как строгое равенство. А если какое-то из ограничений исходной задачи на ее оптимальном решении выполняется как строгое неравенство, то соответствующая компонента оптимального решения двойственной задачи обязательно равна нулю.

Так как балансовая переменная второго ограничения (х6) отлична от нуля, следовательно оно выполняется на оптимальном решении как строгое неравенство, а поэтому у2=0. Так как х1 и х3 отличны от нуля, то получаем следующую систему уравнений: 3*у1 +6*у3 = 48

4*у1 + у3 = 29

Решая их, получаем оптимальные решения двойственной задачи: у1=6, у2=0, у3=5.

1.3 Задача о комплектном плане.

Имеем соотношения: x3:x1= 1; x4:x2=3 или х3=х1; х4=3*х2. Подставив эти выражения, получим задачу ЛП с двумя переменными.

77*х1 +60*х2 à max

7*х1 +11*х2 ≤ 198

3*х1 + 9*х2 ≤ 96

7*х1 + 5*х2 ≤ 228

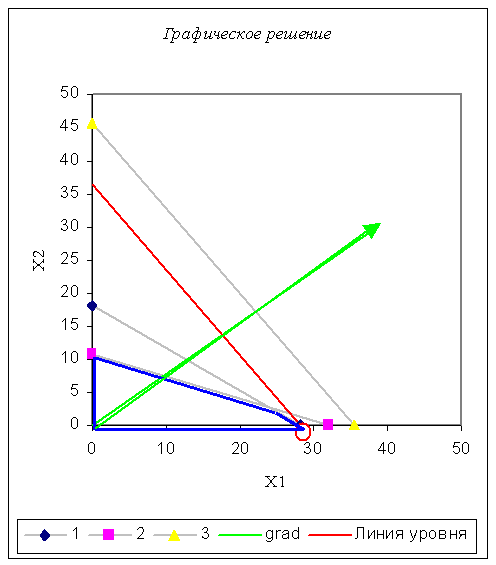
Наносим эти ограничения на плоскость х1х2 и ищем на допустимом множестве максимум функции. Для этого строим градиент grad(77,60). Искомая точка с координатами х1=0; х2»28.29 и максимум прибыли max»2178.

1.4 Оптимальное распределение инвестиций.

Имеем: 4 фирмы, инвестиции в размере 700 тыс. рублей. По этим 4 фирмам их нужно распределить. Размер инвестиций кратен 100 тыс. рублей. Эффект от направления i-й фирме инвестиций в размере m (сотен тыс. рублей) выражается функцией fi(m). Приходим к задаче:

f1(x1)+f2(x2)+f3(x3)+f4(x4)-->max

x1+x2+x3+x4<=7

x1,x2,x3,x4>=0

где xi - неизвестный размер инвестиций i-й фирме. Эта задача решается методом динамического программирования: последовательно ищется оптимальное распределение для k=2,3 и 4 фирм. Пусть первым двум фирмам выделено m инвестиций, обозначим z2(m) величину инвестиций 2-й фирме, при которой сумма f2(z2(j))+f1(m-z2(j)), 0<=j<=m максимальна, саму эту максимальную величину обозначим F2(m). Далее действуем также: находим функции z3 и F3 и т.д. На k-ом шаге для нахождения Fk(m) используем основное рекуррентное соотношение:

Fk(m)=max{fk(j)+F{k-1}(m-j): 0<=j<=7}

Исходные данные:

Таблица №1.

x	100	200	300	400	500	600	700
f1(x1)	28	45	65	78	90	102	113
f2(x2)	25	41	55	65	75	80	85
f3(x3)	15	25	40	50	62	73	82
f4(x4)	33	33	42	48	53	56	58

Заполняем следующую таблицу. Значения f2(x2) складываем со значениями F1(m-x2) = f2(m-x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем и указываем соответствующее значение z2.

Таблица №2.

	m-x2	0	100	200	300	400	500	600	700
x2	f2(x2)/ F1(m-x2)	0	28	45	65	78	90	102	113
0	0	0	28	45	65	78	90	102	113
100	25	25	53	70	90	103	115	127
200	41	41	69	86	106	119	131
300	55	55	83	100	120	133
400	65	65	93	110	130
500	75	75	103	120
600	80	80	108
700	85	85