Количественные методы в управлении
Страница 5
матрица рисков
|
Варианты (ситуации) |
max |
Сэвидж | ||||
|
Решения |
2 |
5 |
6 |
4 |
6 | |
|
0 |
3 |
4 |
2 |
4 | ||
|
2 |
2 |
2 |
2 |
2 | ||
|
0 |
0 |
0 |
0 |
0 |
0 |
Правило Вальда называют правилом крайнего пессимизма: ЛПР уверен, что какое-бы решение он ни принял, ситуация сложится для него самая плохая, так что, принимая i-е решение, он получит минимальный доход q[i]=min{q[i,j]:j=1 4}. Но теперь уже из чисел q[i] ЛПР выбирает максимальное и принимает соответствующее решение.
По правилу Сэвиджа находят в каждой строке матрицы рисков максимальный элемент r[i] и затем из чисел r[i] находят минимальное и принимают соответствующее решение.
По правилу Гурвица для каждой строки матрицы доходов находят величину z[i]=l*max{q[i,j]:j=1 4}+(1-l)*min{q[i,j]:j=1 4}, потом находят из чисел z[i] наибольшее и принимают соответствующее решение. Число l каждый ЛПР выбирает индивидуально - оно отражает его отношение к доходу и риску, при приближении l к 0 правило Гурвица приближается к правилу Вальда, при приближении l к 1 - к правилу розового оптимизма, в нашем случае l равно 1/3.
Итак, по правилу Вальда нам следует принять либо 2-ое, либо 4-ое решение. Сэвидж и Гурвиц нам советуют принять 4-ое решение.
Пусть теперь нам известны вероятности ситуаций - p[j]. Имея матрицу доходов Q теперь можно сказать, что доход от i-го решения есть с.в. Q[i] с доходами q[i,j] и вероятностями этих доходов p[j]. Кроме того, риск i-го решения также есть с.в. R[i] с рисками r[i,j] и вероятностями этих рисков p[j].
Тогда М(Q[i]), М(R[i]) - средний ожидаемый доход и средний ожидаемый риск i-го решения. Принимать решение (проводить операцию) нужно такое, у которого наибольший средний ожидаемый доход, или наименьший средний ожидаемый риск.
|
Варианты (ситуации) |
М(Q[i]), М(R[i]) | ||||||||
|
Доходы |
0 |
1 |
2 |
8 |
2 | ||||
|
2 |
3 |
4 |
10 |
4 | |||||
|
0 |
4 |
6 |
10 |
4 | |||||
|
2 |
6 |
8 |
12 |
6 | |||||
|
Риски |
2 |
5 |
6 |
4 |
4 | ||||
|
0 |
3 |
4 |
2 |
2 | |||||
|
2 |
2 |
2 |
2 |
2 | |||||
|
0 |
0 |
0 |
0 |
0 | |||||
|
p[j] |
1/3 |
1/3 |
1/6 |
1/6 | |||||
М(Q[i])= S (q[i,j]* p[j]) М(R[i])= S (r[i,j]* p[j])
Голубым цветом выделен наибольший средний ожидаемый доход (4-ое решение), а красным цветом – наибольший средний ожидаемый риск (4-ое решение). Как видим, они соответствуют одному и тому же решения. Его и следует принять.
Операции: 1-я – (4;2), 2-я – (2;4), 3-я – (2;4), 4-я – (0;6).
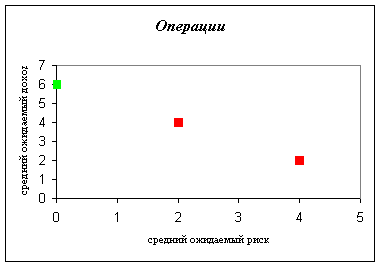
Красным цветом высвечены доминируемые точки (операции), а зеленым – недоминируемые, т.е. оптимальные по Парето. Оптимальной по Парето является 4-я операция.
Была проведена пробная операция, которая значительно сместила распределение вероятностей.
|
Варианты (ситуации) |
М(Q[i]), М(R[i]) |
М*(Q[i]), М*(R[i]) | |||||
|
Доходы |
0 |
1 |
2 |
8 |
2 |
7,2 | |
|
2 |
3 |
4 |
10 |
4 |
9,2 | ||
|
0 |
4 |
6 |
10 |
4 |
9 | ||
|
2 |
6 |
8 |
12 |
6 |
11 | ||
|
Риски |
2 |
5 |
6 |
4 |
4 |
3,8 | |
|
0 |
3 |
4 |
2 |
2 |
1,8 | ||
|
2 |
2 |
2 |
2 |
2 |
2 | ||
|
0 |
0 |
0 |
0 |
0 |
0 | ||
|
p[j] |
1/3 |
1/3 |
1/6 |
1/6 | |||
|
p*[j] |
0,1 |
0 |
0 |
0,9 | |||