Курсовая работа по ЭММ

Страница 3

5. Переходим к новой таблице. Для этого отмеченную строку умножаем на ( чтобы на месте разрешающего элемента появилась единица) и пишем ее на месте прежней. К каждой из остальных строк таблицы прибавляем строку, полученную на месте отмеченной строки, умноженную на такое число, чтобы элемент, стоящий в отмеченном столбце, обратился в 0.

6. С новой таблицей возвращаемся к п.2

1.3 М-метод.

Для решения М-задачи можно воспользоваться симплекс-методом, поскольку указан допустимый базис.

При решении М-задачи могут представиться две возможности:

1. М-задача имеет решение, т.е. min F существует.

2. М-задача не имеет решения, min F =¥.

Решая М-задачу, мы стремимся получить оптимальное решение, в котором значения искусственных неизвестных равны нулю. Для того чтобы этого достичь, необходимо выбрать последовательность шагов таким образом, чтобы все искусственные неизвестные вышли из базиса, т.е. стали свободными. Тогда в базисном решении значения этих неизвестных и будут как раз нулями.

Таким образом, переходя при решении М - задачи от одного базиса к другому, мы стараемся в первую очередь выводить из базиса одно искусственное неизвестное за другим. Возможны, впрочем, и такие (досадные) случаи, когда в процессе решения приходится заменять одно искусственное неизвестное на другое (выбор разрешающего элемента по-другому не получается). Но общим направлением вычислительного процесса во всех случаях остается постепенный вывод искусственных неизвестных из базиса.

1.4 Двойственные задачи .

С каждой задачей линейного программирования связана другая задача, называемая двойственной по отношению к исходной. Совместное изучение данной задачи и двойственности к ней дает, как правило, значительно больше информации.

Задачи I и I’ называются двойственными друг другу. Смысл, который вкладывается в это название, состоит в следующем.

1. Если первая задача имеет размеры m x n ( m ‑ ограничений с n неизвестными), то вторая - размеры n x m.

2. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными .

3. В правых частях ограничений в каждой задаче стоят коэффициенты при неизвестных в целевой функции другой задачи.

4. В задаче I все ограничения представляют собой неравенства типа £, причем в этой задаче требуется достичь max f. Напротив, в задаче I’ все ограничения суть неравенства типа ³, причем требуется достичь min j.

Двойственная задача заключается в минимизации общей оценки всего имеющегося количества ресурсов.

Взаимозависимость оптимальных решений пары двойственных задач определена следующими теоремами:

Теорема (основное неравенство). Пусть Х - какое-нибудь допустимое решение задачи I, т.е. любое решение системы, а Y - какое-нибудь допустимое решение задачи I’ - любое решение системы. Тогда справедливо неравенство

f(Х) £j(Y).

Следствие1 (достаточный признак оптимальности). Если для каких-то допустимых решени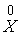й и 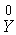задач I и I’ выполняется равенство

f(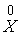)=j(),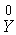

то 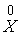есть оптимальное решение задачи I, а 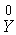- оптимальное решение задачи I’.

Следствие2. Если в одной из задач I и I’ целевая функция не ограничена с соответствующей стороны (т.е. max f = ¥ в задаче I или min j = -¥ в задаче I’), то другая задача не имеет допустимых решений.

Основная теорема. Если разрешима одна из двойственных задач I или I’, то разрешима и другая задача, причем max f = min j.

Теорема равновесия. Пусть Х и Y- допустимые решения задач I и I’. Для оптимальности (одновременной) этих решений необходимо и достаточно выполнение равенств

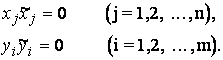
Решение двойственной задачи находится в строке Dj симплекс-таблицы в последних столбцах дополнительных переменных. Переменные yi обозначают оценки одной единицы ресурса.

Величина двойственной оценки того или иного ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу.

Двойственные оценки измеряют эффективность малых приращений объемов ресурсов в конкретных условиях данной задачи. Если целью является расширение производства и повышение эффективности плана путем привлечения дополнительных ресурсов, то анализ оценок поможет выбрать правильное решение. Прирост различных ресурсов будет давать неодинаковый эффект, т.е. оценки позволяют с большей точностью выявить узкие места, сдерживающие рост эффективности производства. С учетом всех конкретных условий задачи оценки показываю, какие ресурсы более дефицитны, какие менее дефицитны и какие избыточны. Дефицитные ресурсы имеют самые высокие оценки.

2. Задача планирования производства.

2.1 Определение оптимального варианта строительств скважин в УБР на планируемый год.

1. Постановка задачи.

В УБР запланировано строительство скважин нескольких категорий:

I категории - не более H1;

II категории - не более Н2;

III категории - не менее (не более) Н3.

При строительстве скважин используются разные материально-технические ресурсы, наличие которых в УБР ограниченно следующим количеством (в тоннах):

обсадные трубы - В1;

химреагенты - В2;

глина и глинопорошок - В3;

талевый канат - В4;

ГСМ - В5.

При строительстве скважин разной категории потребляется различное количество ресурсов каждого вида. Расход материально-технических ресурсов в расчете на одну скважину каждой категории задан таблицей 1.

Таблица 1

категории скважин		виды ресурсов
	Обсадные трубы	Х/реагенты	глина и глинопорошок	Талевый канат	ГСМ
I	450	45	130	20	46
II	300	40	110	16	36
III	200	30	70	15	30

Экономический эффект при строительстве скважины j категории определен Эj тыс. руб.

Требуется:

1. Определить оптимальный план строительства скважин, при котором в пределах ограниченного объема ресурсов (табл.1) достигается максимальный экономический эффект.

2. Определить двойственные оценки ресурсов и их устойчивость.

3. Провести всесторонний анализ полученных оптимальных решений.

Таблица 2

Н1	Н2	Н3	Э1	Э2	Э3	В1	В2	В3	В4	В5
15	9	не менее 9	186	125	90	4800	600	1610	280	580