Оптимизация рациона кормления скота
Страница 4
Как видно из данной таблицы, самым дорогими кормами (с точки зрения стоимости единицы питательного вещества) являются корнеклубнеплоды (а именно, полусахарная свёкла). Поэтому входят в рацион в минимальных количествах. Самым дорогим кормом из концентратов является виковая мука. Она входит в рацион в небольшом количестве (1,992 кг). Другой концентрат – жмых льняной незначительно дешевле, поэтому он также входит в рацион в сравнительно небольшом количестве. Самыми дешевыми являются грубые корма, которые в рационе представлены сеном клеверным, и турнепс.
1.3.Выводы
Таким образом, рассчитав нашу модель и, получив минимизированный результат при помощи программного пакета Microsoft Office 2000, я сделал вывод, что полученный результат является оптимальным и минимизирует наши затраты. При этом полностью удовлетворяется потребность коровы в питательных веществах и их соотношениях.
Если бы при расчетах не использовалась математическая модель, то решение находилось бы очень долго и полученный результат, возможно, не был бы оптимальным.
Итак, метод линейной оптимизации очень удобен для решения задач, к примеру, животноводческих ферм.
2. Примеры решения задач производственными функциями
2.1. Системный и качественный анализ факторов и выбор критерия оптимальности.
Для рассмотрения корреляционно-регрессионного анализа нужно сначала рассмотреть что такое производственная функция, итак производственная функция - модель выражающая взаимосвязь факторов производства с его результатами. В общем случае производственную функцию можно представить в виде:
Y = F(X1, X2, … Xn)
Производственные функции находят свое применения не только на отдельном предприятии, а применяются почти везде, к примеру их можно встретить в сельском хозяйстве, промышленности. В качестве факторов производства могут использоваться различные показатели: национальный доход, валовый общественный продукт, а на микроуровне – показатели производительности труда, нормативные затраты, затраты рабочей силы. Многофакторные производственные функции имеют наибольшую ценность для планирования производства, т.к. позволяют оценить влияние большого количества факторов на результат производства, но для таких функций требуется большое количество объектов для анализа и большая точность проводимых наблюдений. Рассмотрим метод производственной функции на конкретном примере.
Предположим, что итоговым результирующим показателем деятельности предприятия является уровень производительности труда (тыс. руб. /чел.)
Допустим, что нам даны следующие факторы, которые по предположению должны оказывать влияние на производительность труда:
X1 – Коэффициент сменности оборудования
X2 – Среднегодовой фонд оплаты труда промышленно-производственного персонала предприятия (тыс. руб. /чел.)
X3 – Уровень фондовооруженности труда (тыс. руб. /чел.)
В результате исследований 20-ти предприятий были получены следующие данные:

На основании вышеприведенных данных будут производиться все дальнейшие расчеты.
2.2. Предварительное исследование корреляционной связи
Перед непосредственным корреляционно-регрессионным анализом и построением производственной функции необходимо предварительно оценить сам факт существования связи между результатом и факторами. Наиболее эффективным способом такой оценки, на мой взгляд, является графический способ.
Построим три графика отображающих зависимость конечного результата, т.е. производительности труда, от всех факторов.
График 1
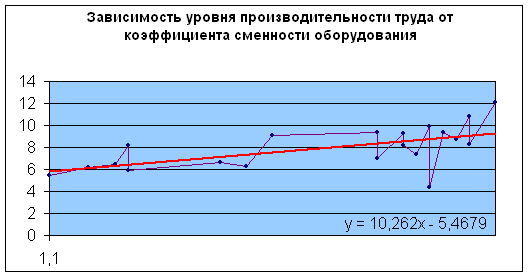
На этом графике можно проследить за зависимостью между ростом коэффициента сменности оборудования и увеличением уровня производительности труда .
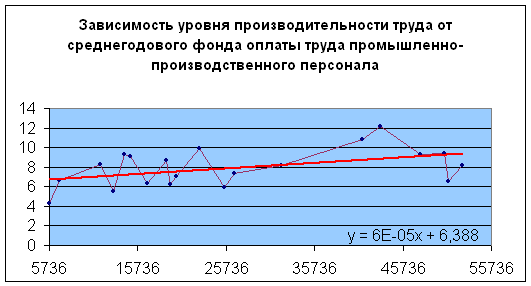
На данном графике видно, что с ростом фонда оплаты труда – растет и уровень производительности. 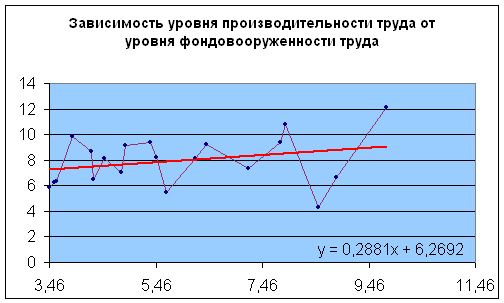
При возрастании уровня фондовооруженности растет и уровень производительности труда.
Не смотря на приведенные графики, на которых возможно отследить зависимость, мы проведем более тщательное исследование, т.к. в графическом виде четко отобразить связь не получится.
|
|
Y |
X1 |
X2 |
X3 |
|
Среднее значение |
952,6 |
0,25 |
45783211924
|
70,9 |
|
Среднее квадратическое отклонение |
30,9 |
0,50 |
66763 |
8,4 |
|
Коэффициент вариации |
0,04%
|
2,64% |
0,39% |
0,69% |
По полученным данным можно сказать, что все значения имеют очень маленький разброс наблюдений, для нормального распределения необходимо, чтобы коэффициент корреляции должен быть равен 33%.
2.3. Анализ и решение данной модели
Для быстроты вычисления и удобства анализ, я воспользовался ЭВМ, т.к. имеющиеся пакеты программ позволяют разрешить поставленную задачу.
+-----------------------------------------------------------------------------+
МНОГОФАКТОРНЫЙ КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
+-----------------------------------------------------------------------------+
3-х факторный корреляционный анализ
Исходная матрица:
1 2 3 4
1 9.260 1.370 47740.000 6.400
2 9.380 1.400 50391.000 7.800
3 12.110 1.440 43149.000 9.780
4 10.810 1.420 41089.000 7.900
5 9.350 1.350 14257.000 5.350
6 9.870 1.390 22661.000 3.900
7 8.170 1.160 52509.000 4.500
8 9.120 1.270 14903.000 4.880
9 5.880 1.160 25587.000 3.460
10 6.300 1.250 16821.000 3.600
11 6.220 1.130 19459.000 3.560
12 5.490 1.100 12973.000 5.650
13 6.500 1.150 50907.000 4.280
14 6.610 1.230 6920.000 8.850
15 4.320 1.390 5736.000 8.520
16 7.370 1.380 26705.000 7.190
17 7.020 1.350 20068.000 4.820
18 8.250 1.420 11487.000 5.460
19 8.150 1.370 32029.000 6.200
20 8.720 1.410 18946.000 4.250
Корреляционная матрица:
1 2 3 4
1 1.000 .602 .467 .287
2 .602 1.000 .044 .491
3 .467 .044 1.000 .106
4 .287 .491 .106 1.000
Множественная регрессия и одномерные статистики
--------------------------------------------------------------------------------
## Множественная Одномерные
переменных регрессия статистики
Коэфф. регр. Станд. ош. Средние Станд. откл.
--------------------------------------------------------------- Зависимая 7.9450 1.9380
Независим 1 10.4417 3.2450 1.3070 .1137
2 .0001 .0000 26716.8500 15523.0300
3 -.0617 .1920 5.8175 1.9316
--------------------------------------------------------------------------------
Свободный член уравнения регрессии = -6.8321
Множественный коэфф. корреляции = .7482
Множественный коэфф. детерминации = .5598
Стандартная ошибка ур. регр. = 1.4012
F-значение = 6.7828
Число степеней свободы для воспр. дисперсии = 3
для остат. дисперсии = 16
Бета-коэффициенты:
.6128 .4463 -.0615
Значения T-Стьюдента:
3.2178 2.6754 -.3214
Коэффициенты отдельного определения:
.3691 .2083 -.0177
Коэффициенты эластичности:
1.7177 .1874 -.0452