Математические модели в программе логического проектирования
Страница 10
zq=fq(xn, ,x1),
где zq- выходные сигналы комбинационной схемы,
xp- входные сигналы, p= 1, 2, .,n, q= 1, 2, ,k;
описывающая работу комбинационной схемы(КС) без обратных связей, является её статической моделью.
Для исследования переходных процессов, вызываемых в логических схемах(ЛС) изменениями входных сигналов, необходимо ввести динамические модели ЛЭ, учитывающие паразитные задержки. Тогда динамическая модель ЛС будет определятся динамической моделью ЛЭ и статической моделью ЛС. Так, динамическая модель КС без обратных связей будет определятся формой представления функций fq(v), задающей структурную схему (число ЛЭ и все связи между ними), и динамической моделью ЛЭ.
Самая общая динамическая модель ЛЭ И-НЕ, имеющего два входа, представлена на рис.3.1(а).
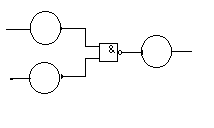 а)
а)
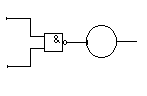 б)
б)
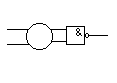 в)
в)
Рис.3.1 Модели логического элемента ИЛИ-НЕ
Эта модель состоит из безынерционного ЛЭ И-НЕ (статическая часть модели) и паразитных элементов задержки (i=1, 2, 3). Величины задержек и зависят от длины проводников, соединяющих выводы ЛЭ с источниками сигналов, от длительности фронтов входных сигналов x1 и x2, от порогов срабатывания ЛЭ по входам x1 и x2, а величина определяется инерционностью той части ЛЭ И-НЕ, через которую проходит сигнал описываемый функцией x1 x2 .В общем случае точные значения величин i неизвестны, так как они зависят от многих факторов и стечением времени могут изменяться. Кроме того, значения величин i могут быть различными при переходах сигналов x1, x2 и с 0 на 1 и с1 на 0. Рассмотренная модель является наиболее сложной и пригодна для описания любого ЛЭ (И, ИЛИ, ИЛИ-НЕ), если использовать в ней соответствующую статическую модель.
Будем говорить, что входные сигналы ЛЭ не изменяются одновременно, если на интервале изменяется только один сигнал x1 или x2 , и что входные сигналы ЛЭ изменяются одновременно, если на интервале изменяются оба сигнала x1 и x2, так как истинное соотношение величин задержек и неизвестно. Если сигналы x1 и x2 никогда одновременно не изменяются (хотя бы в противоположных направлениях), то модель ЛЭ И-НЕ может быть приведена к виду, показанному на рис.3.1(б), где - элемент задержки с переменной величиной задержки или в зависимости от того, каким сигналом xp вызывается изменение выходного сигнала . Поэтому данную модель назовём динамической моделью с переменной задержкой. Из рис 3.1(б) следует, что:
Обозначив сигналы xp(t)= xp и , получим :
где - значение выходного сигнала ЛЭ в данный момент времени,
- следующее его значение, которое появится через времям
после изменения входных сигналов xp.
Модель с переменной задержкой можно представить в несколько ином виде (рис.3.1(в)), положив, что элемент задержки в момент изменения сигнала xp подключается к тому входу, на который этот сигнал подаётся, а на другом входе элемент задержки в этом случае отсутствует. Данную модель будем называть динамической моделью с виртуальной задержкой.
Логический элемент находится в устойчивом состоянии, если сигналы до элемента задержки и после него совпадают, т.е. если . Если же , то ЛЭ находится в неустойчивом состоянии, так как в этом случае его выходной сигнал должен изменится через время не большее .
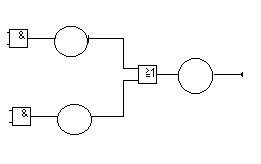 а)
а)
б)
Рис.3.2 Комбинационная схема составленная из логических элементов И и ИЛИ на основании их динамических моделей
На рис.3.2(а) показана КС, составленная из ЛЭ И и ИЛИ на основании их динамических моделей. Для ЛЭ И использована модель с переменной задержкой, а для ЛЭ ИЛИ - общая модель. Как видно из рис.3.2(а), КС выполняет функцию f(v)=x3 x1+x3 x2, которая является её статической моделью.
Пусть x1= x2=1 и изменяется только один сигнал x3. Тогда функция f(v)=x3 +x3 =1, т.е. из статической модели КС следует, что её выходной сигнал не должен изменятся при изменениях входного сигнала x3. Наличие же паразитных задержек и разной величины приводит к появлению на выходе КС ложных значений выходного сигнала малой длительности (рис.3.2(б)). Так как истинное соотношение величин задержек и неизвестно, то нельзя предугадать, в каком месте появится ложное значение выходного сигнала (при изменении входного сигнала x3 с 0 на 1 или с 1 на 0). Динамические модели ЛЭ и предназначены для формализации исследования поведения ЛС при переходных процессах, вызываемых в них изменениями входных сигналов.
При изменении выходных сигналов двух или большего числа ЛЭ, вызванных одними и теми же изменениями входных сигналов КС, из-за неравенства задержек возникают состязания(гонки) ЛЭ. Состязания ЛЭ называются критическими, или недопустимыми, если хотя бы один выходной сигнал КС во время переходного процесса может изменится более одного раза. Состязания ЛЭ называются некритическими, или допустимыми, если все выходные сигналы КС во время переходного процесса изменяются только один раз.
4. Разработка логических схем практикума
Представленные ниже электрические схемы являются примерами схем синтезируемых в ходе выполнения лабораторной работы.
4.1 Схема цифрового автомата
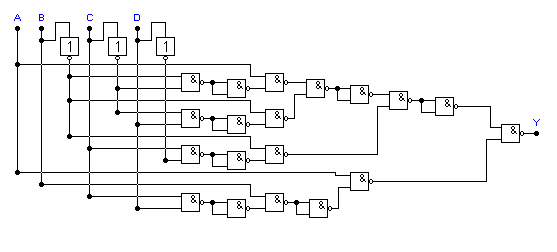
Рис.4.1 Логическая схема к 1-му варианту
Схема изображённая на рис.4.1 представляет из себя цифровой автомат (с 4-мя входами A, B, C и D и выходом Y) реализующий логическое уравнение:
Y=ABC+BCD+BCD+ABCD
Настоящая схема реализована в базисе И-НЕ при помощи логического конвертора.
4.2 Цифровой компаратор 2-х разрядного кода
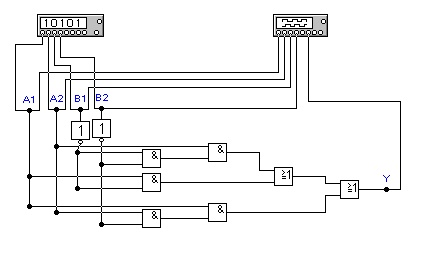
а)
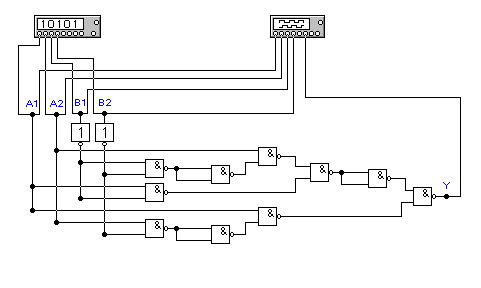
б)
Рис.4.2 Схема цифрового компаратора ко 2-му варианту
На рис.4.2(а,б) изображена схема цифрового компаратора. Входными кодами являются 2-х разрядные коды А и В (А1,А2 и В1, В2 соответственно). Реализуемая им логическая функция имеет вид:
Y=1 если A>B
Схема реализована в двух доступных в логическом конверторе базисах: рис.4.2(а) И, ИЛИ, НЕ и рис.4.2(б) И-НЕ. Для контроля правильности работы компаратора в обе схемы введены генератор слов и логический анализатор. Генератор слов подключен на входах схем и используется для генерации всех возможных комбинаций кодов А и В (2 разряда код А и 2 код В всего 4, следовательно 24=16 - генерируется 16 различных слов). На выходах схем подключен логический анализатор причём его первые 4 канала включены параллельно 4 используемым выходам генератора слов. Это сделано для получения более наглядной картинки на экране панели управления логического анализатора(см рис.4.3)
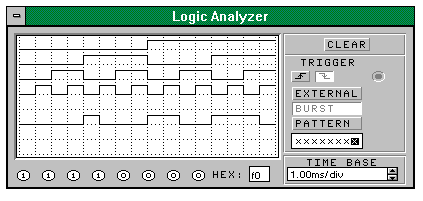
Рис.4.3 Временная диаграмма работы цифрового компаратора
Выход схемы подключен к 6-му каналу анализатора. Таким образом на экране одновременно отображаются входные и выходные сигналы, что позволяет получить полную временную диаграмму работы устройства(вход и выход на экране точно синхронизированы во времени).Наименование каналов сверху вниз: А1, А2, В1, В2 и Y.
4.3 Дешифратор 4-х разрядного адреса
 а)
а)
 б)
б)
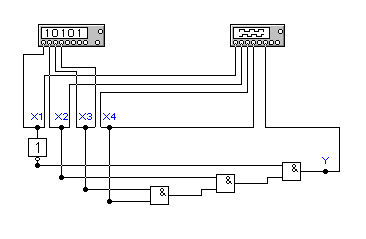
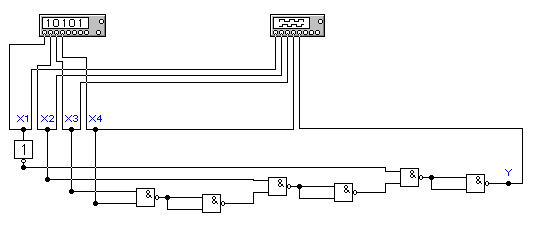
Рис.4.4 Схема дешифратора адреса к 3-му варианту.
На рис.4.4(а,б) показана схема дешифратора адреса. Причём на рис.4.4(а) схема синтезирована в базисе И, ИЛИ, НЕ, а на рис.4.4(б) в базисе И-НЕ. Дешифрируемый адрес 01112 или 710. Подключив на вход схем генератор слов, а на выход логический анализатор(точно также как и в предыдущей схеме) легко получить временные диаграммы работы устройства см.рис.4.5
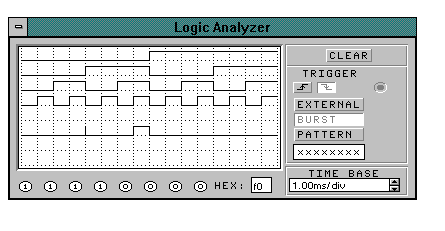
Рис.4.5 Временные диаграммы дешифратора адреса
С полученных временных диаграмм легко сосчитать дешифрованный адрес. Кроме того на полученной диаграмме выхода схемы можно наблюдать паразитный выброс - результат гонок возникающих с приходом кода 0100 на первом элементе И см.рис.4.4(а). Это вполне объяснимо поскольку разряды дешифрируемого сигнала проходят разное количество цифровых элементов. Конечно у реальных дешифраторов обязательно используется строб-импульс или тактирование.