Математическое моделирование в сейсморазведке
Страница 9
Данное уравнение имеет место лишь в рамках акустического приближения, поэтому его решение содержит только продольные волны.
Трансформируя поверхность S в полусферу с бесконечным радиусом, на диаметральной плоскости которой расположен отражающий элемент, и аппроксимируя отражающую поверхность набором плоских полос бесконечной длины и шириной Dx=x2 – x1 (рис. 10, а), А. Трорей получил решение дифракционного интеграла (4.3) для одной[1] такой полосы в виде
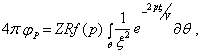 (4.4)
(4.4)
здесь R – коэффициент отражения; f(р) – преобразование Лапласа от импульса волны в источнике Q; смысл обозначений Z, q и x ясен из рис. 10. a. Для интегрирования выражения (4.4) следует выразить x через угол q (рис. 10, a), однако два важных вывода можно сделать и до этого
1. На каждом краю отражающего (дифрагирующего) элемента (в точках А рис. 10, б) фаза дифракции изменяется на 180°. В самом деле, пусть D1 и D2 – результаты интегрирования (4.4) в направлении линии АВ (рис. 10, а) на расстоянии Х1 и Х2 соответственно (в пределах от -p/2 до p/2). Тогда jр=D2-D1. Если Х1<0, что соответствует положению точки p над полосой, то jр=V–D2–D1 (здесь V обозначен член, соответствующий отражению). Отсюда следует, что D2 меняет знак при переходе Р через край полосы.
2. На дифрагирующем краю форма отраженной и форма дифрагированной волн совпадают, но величина амплитуды дифрагированной волны в 2 раза меньше. Действительно, пусть точка Р при движении слева направо пересекает дифрагирующую полосу (рис. 10, б). Для распространения алгоритма Трорея на случай многослойной среды с криволинейными Распределение амплитуд показано на этом же рисунке. Из условий непрерывности jр при переходе через край А имеем D2=V–D2, т.е. D2=V/2, что и требовалось.
3. Границами раздела, с горизонтальным градиентом пластовых скоростей и плотностей, с угловыми несогласиями и выклиниваниями Ф. Хилтерман предложил вычислительный способ приведения среды над каждой границей поочередно к однослойной с единой постоянной скоростью. Для этой цели из каждого пункта наблюдения с равным шагом по углу производится трассирование лучей в исходной модели, после чего каждый прослеженный луч заменяется прямолинейным лучом, выходящим из пункта наблюдения под тем же углом (рис. 10, в). Мнимое положение края плоского элемента рассчитываемой границы с номером j находится на прямолинейном луче на расстоянии, равном 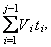 где Vi – локальная скорость; ti – время прохождения трассированного луча в i-м слое (соответствующий пример представлен на рис. 10, в для границы 3). Множество всех полученных таким образом мнимых точек образует мнимую модель, состоящую из одной границы с одной постоянной скоростью. От всех краев плоских элементов, составляющих эту мнимую границу, дифрагированные волны правомерно рассчитывать по "простой теории" Трорея.
где Vi – локальная скорость; ti – время прохождения трассированного луча в i-м слое (соответствующий пример представлен на рис. 10, в для границы 3). Множество всех полученных таким образом мнимых точек образует мнимую модель, состоящую из одной границы с одной постоянной скоростью. От всех краев плоских элементов, составляющих эту мнимую границу, дифрагированные волны правомерно рассчитывать по "простой теории" Трорея.
Раздел 4.3. Количественное оценивание сходства трасс синтетического и реального временных разрезов
Как отмечено в разд. 3.4, при реализации технологии интерпретации данных сейсморазведки, основанной на математическом моделировании, используются оценки сходства, имеющие интегральный и дифференциальный характер.
§ 4.3.1. Способы вычисления предварительных оценок
В качестве первоначальной оценки сходства отрезков сейсмических трасс, входящих в соответствующие друг другу сегменты применяется интегральная оценка с помощью широко известной нормированной функции взаимной корреляции вида:
 ,
,
где Ар и Ас – отсчеты реальной и синтетической трасс; L – длина сравниваемых трасс; п – номер отсчета сравниваемых трасс; q = –(L–1), –(L–1)+1, …, (L–1) – сдвиг. Из формулы видно, что р(q) Î [-1, 1], причем случай р = ±1 соответствует полному подобию АP(t) и Ас(t) с точностью до полярности, а р=0 – полной их некоррелированности.
Оценка сходства R для заданных трасс и временные сдвиги между ними получаются в результате обработки НФВК р(q) по следующему алгоритму.
1) выделяются все положительные максимумы НФВК;
2) в координатах (р, q) строится окно поиска [(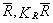 ), ± КТ
), ± КТ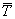 ], где
], где 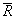 – средняя амплитуда всех экстремумов рассматриваемой функции;
– средняя амплитуда всех экстремумов рассматриваемой функции; 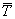 – средний период (среднее расстояние между экстремумами); КR и КT – задаваемые константы;
– средний период (среднее расстояние между экстремумами); КR и КT – задаваемые константы;
3) за оценку R принимается наибольший из всех положительных экстремумов НФВК, попадающих в окно поиска;
4) в случае, если указанное окно не содержит ни одного положительного экстремума, считается, что между сравниваемыми трассами сходство полностью отсутствует; аналогично интерпретируется и случай, когда в окне имеются два и более положительных экстремумов с примерно равными амплитудами, которые характеризуют минимальный уровень значимости параметра R.
В качестве простейшей дифференциальной оценки сходства используется разность между численными производными сравниваемых отрезков сейсмических трасс, при этом для большей устойчивости численные производные сглаживаются путем суммирования на малой базе Вz. Конкретно, вычисляется модульная оценка:
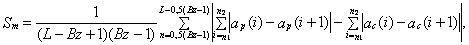
где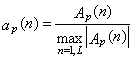 ,
,  , n1=п – 0,5(Вz–1), n2=п + 0,5(Вz–3) – нормированные амплитудные значения отрезков трасс РВР и СВР, а также квадратичная оценка Ssq, отличающаяся от предыдущей тем, что вместо модуля разности сумм в ней используется квадрат этой разности. Понятно, что нулевые значения этих оценок соответствуют полному сходству кривых (по используемому критерию); рост значений этих оценок соответствует нарастанию их несходства.
, n1=п – 0,5(Вz–1), n2=п + 0,5(Вz–3) – нормированные амплитудные значения отрезков трасс РВР и СВР, а также квадратичная оценка Ssq, отличающаяся от предыдущей тем, что вместо модуля разности сумм в ней используется квадрат этой разности. Понятно, что нулевые значения этих оценок соответствуют полному сходству кривых (по используемому критерию); рост значений этих оценок соответствует нарастанию их несходства.
§ 4.3.2. Способ построения дифференциальных оценок, основанный на анализе характерных точек трасс СВР и РВР
При формировании репрезентативной системы частных критериев сходства используются следующие предположения:
1) в процессе визуального сопоставления трасс СВР и РВР геофизик-интерпретатор выделяет так называемые характерные точки этих кривых – нули и экстремумы;
2) визуальное сопоставление каждой пары трасс основывается на следующих непосредственно воспринимаемых геофизиком-интерпретатором факторах: общее число и порядок следования характерных точек, соотношение амплитуд экстремумов, разница в положении абсцисс характерных точек.
Согласно следующему предположению искомая система частных критериев сходства двух кривых А(1)(t) и А(2)(t), являющихся отрезками трасс РВР и СВР соответственно, включает в себя безразмерные критерии четырех типов:
1) рассогласование в соотношениях амплитуд сопоставленных друг другу экстремумов (рис. 11): 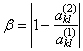 ,
, 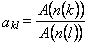 , где k и l – порядковые номера этих экстремумов, отсчитанные от начала рассматриваемого временного интервала; п(k) и п(l) – соответствующие им номера отсчетов в дискретизированном представлении кривых;
, где k и l – порядковые номера этих экстремумов, отсчитанные от начала рассматриваемого временного интервала; п(k) и п(l) – соответствующие им номера отсчетов в дискретизированном представлении кривых;
2) рассогласование в относительном положении сопоставленных экстремумов на полупериоде: 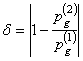 ,
, 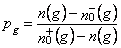 . Где g – порядковый номер данного экстремума среди других экстремумов, зафиксированных в рассматриваемом временном интервале; п(g) – номер соответствующего ему отсчета; смысл
. Где g – порядковый номер данного экстремума среди других экстремумов, зафиксированных в рассматриваемом временном интервале; п(g) – номер соответствующего ему отсчета; смысл 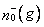 и
и 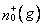 ясен из рис. 11;
ясен из рис. 11;
3) рассогласование в ширине полупериода: 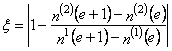 , где e – порядковый номер нуля функций А(t), c которого начинается данный полупериод, среди других нулей, выделенных в рассматриваемом интервале, а смысл остальных обозначений ясен из рис. 11;
, где e – порядковый номер нуля функций А(t), c которого начинается данный полупериод, среди других нулей, выделенных в рассматриваемом интервале, а смысл остальных обозначений ясен из рис. 11;