Метод ветвей и границ

Страница 2

Таким образом исходная задача целочисленного программирования имеет оптимальный план Х*= (3, 1, 2, 3, 3). При этом плане целевая функция принимает максимальное значение .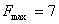

Схему реализованного выше вычислительного процесса можно представить в виде дерева, ветвями которого являются соответствующие ограничения на переменные, а вершинами – решения соответствующих задач линейного программирования (рис 2.5).

Дадим геометрическую интерпретацию решения задачи (50)-(53). На рис. 2.6 показана область допустимых решений задачи (50)-(52).

Из него видно, что данная задача имеет оптимальный план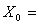(18/5, 3/5, 0, 0, 24/5). В то же время 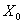не является планом задачи (50)-(53), поскольку три переменные имеют дробные значения. Возьмем переменную х1 и рассмотрим задачи (I) и (II).

Как видно из рис. 2.7задача (I) имеет оптимальный план 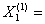(3, 3/2, 0, 9/2, 3/2), а из рис.2.8 следует, что задача (II) неразрешима.

Поскольку среди компонент плана 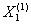есть дробные числа, выберем переменную х2 и рассмотрим задачи (III) (IV). Задача (III) имеет оптимальный план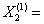(3, 1, 2, 3, 3) (рис. 2.9), а задача (IV) неразрешима (рис. 2.10).

Итак, Х*= (3, 1, 2, 3, 3) является оптимальным планом задачи (50)-(53). При этом плане .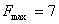

Решение задачи, правые части которых содержат параметр.

Алгоритм решения задачи (60)-(62) подобен рассмотренному выше алгоритму решения задачи (57)-(59).

Полагая значение параметра t равным некоторому числу t0, находим решение полученной задачи линейного программирования (60)-(62). При данном значении параметра t0 либо определяем оптимальный план, либо устанавливаем неразрешимость задачи. В первом случае найденный план является оптимальным для любого, где

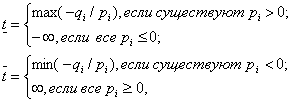
и числа qi и pi определены компонентами оптимального плана и зависят от t0:

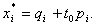
Если при t = t0 задача (60)-(62) неразрешима, то, либо целевая функция задачи (60) не ограничена на множестве планов, либо система уравнений не имеет неотрицательных решений. В первом случае задача неразрешима для всех 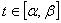, а во втором случае определяем все значения параметра 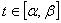, для которых система уравнений (61) несовместна, и исключаем их из рассмотрения.

После определения промежутка, в котором задача (60)-(62) имеет один и тот же оптимальный план или неразрешима, выбираем новое значение параметра t, не принадлежащее найденному промежутку, и находим решение полученной задачи линейного программирования. При этом решение новой задачи ищем с помощью действенного симплекс-метода. Продолжая итерационный процесс, после конечного числа шагов получаем решение задачи (60)-(62).

Итак, процесс нахождения задачи (60)-(62) включает следующие основные этапы:

10. Считая значение параметра t равным некоторому числу 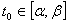, находят оптимальный план или устанавливают неразрешимость полученной задачи линейного программирования.

20. Находят значения параметра 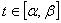, для которых задача (60)-(62) имеет один и тот же оптимальный план или неразрешима. Эти значения параметра t исключают из рассмотрения.

30. Выбирают значения параметра t из оставшейся части промежутка 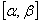и устанавливают возможность определения нового оптимального плана находят его двойственным симплекс-методом.

40. Определяют множество значений параметра t, для которых задача имеет один и тот же новый оптимальный план или неразрешима. Вычисления проводят до тех пор, пока не будут исследованы все значения параметра .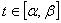

2.66. Для каждого значения параметра 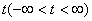найти максимальное значение функции

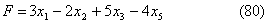
при условиях

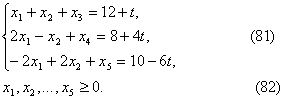
Р е ш е н и е . Считая значение параметра t в системе уравнений (81) равным нулю, находим решение задачи (80)-(82) (табл. 2. 41).

Таблица 2.41

i	Базис	Сб	Р0	3	-2	5	0	-4
Р1	Р2	Р3	Р4	Р5
1	Р3	5	12+t	1	1	1	0	0
2	Р4	0	8+4t	2	-1	0	1	0
3	Р5	-4	10-6t	-2	2	0	0	1
4			20+29t	10	-1	0	0	0
1	Р3	5	7+4t	2	0	1	0	-½
2	Р4	0	13+t	1	0	0	1	½
3	Р2	-2	5-3t	-1	1	0	0	½
4			25+26t	9	0	0	0	½