Коррупция как объект матеметического моделирования
Страница 10
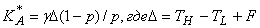 (9)
(9)
Предположеиве 6.
Налогоплательщики нейтральны к риску. Они минимизируют ожидаемые затраты, связанные с уплатой налогов; эти затраты включают сами налоги, взятки, штрафы и наказание за уход от налогов.
Предположим, что наказание за сокрытие дохода для данного налогоплательщики составляет KT, он получил высокий доход, но в отчетности указал низкий. Если его проверяет налоговый инспектор, для которого наказание за взятку составляет KA, причем KA < K*A, т.е. он в принципе берет взятки, но налогоплательщик взятки ему не предлагает, то последний должен будет заплатить TH +F. Если же налогоплательщик решил дать взятку, то его ожидаемые затраты составляют TL + (1 - р)gD + р(D + KT). Следовательно, налогоплательщик предлагает взятку только в том случае, если
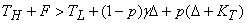 (10)
(10)
Другими словами, налогоплательщик предлагает взятку только, если KT < K*T , где
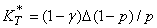 (11)
(11)
Определение 1. Условимся называть налогоплательщика честным, если KT ³ K*T,и нечестным, если KT < K*T.
Обозначим aH вероятность того, что честный налогоплательщик решится уклониться от налогов; aH(KT) - вероятность того, что нечестный налогоплательщик, для которого наказание за взятки составляет KT, скроет свой высокий доход. Поскольку для налоговой инспекции априори все налогоплательщики равны, то р - вероятность проверки низкого дохода - одинаковая для всех. Пуст CH(aH,b) будет функцией общих расходов, которые отнесет честный налогоплательщик, скрывающий свой доход, и CD[aH(KT), b;KT] - функцией расходов нечестного налогоплательщика, уходящего от уплаты налогов, для которого наказание за взятку составляет KT. Тогда,
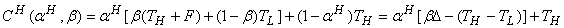 (12)
(12)
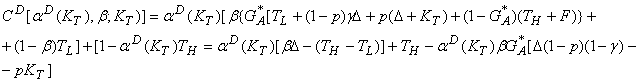
(13)
где 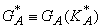 (14)
(14)
Определение 2.
Наилучший ответ для честного неплательщика налогов jH(b) -это величина aH, минимизирующая CH(aH, b). Наилучший ответ нечестного неплательщика jD(b) -это величина aD(KT), минимизируюищя функцию CD[aD(KT), b;KT].
Из линейности СH по aH и СD по aD(KT) следует.
Утверждение 1.
Наилучшим ответом для честного неплательщика налогов является
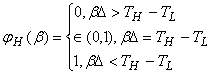 (15)
(15)
Наилучшим ответом нечестного неплательщика будет
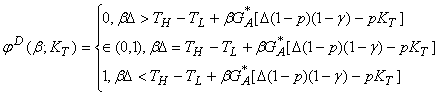 (16)
(16)
Для последующего анализа удобно рассмотреть те вероятности финансовой проверки, которые оставляют честных и нечестных неплательщиков безразличными относительно того, скрывать свой дохоц или нет. Из Утверждения 1 следует
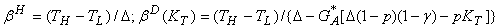 (17)
(17)
Утверждение 2.
bD(KT) > bH для всех KT < K*T, bD(K*T) = bH и dbD(KT)/dKT < 0 (18)
Пусть количество проверок не зависит от конкретных аудиторов, а определяется на более высоком административном уровне. В этой модели действуют два вида налоговых инспекторов - наивные и опытные. Обозначим вероятность проверки, проводимой этими видами инспекторов, как bN и bS соответственно.
Определение 3.
Наивные налоговые инспектора считают, что все налогоплательщики честные. Опытные налоговые инспектора допускают возможность коррупции.
Предположение 7.
Налоговые инспектора нейтральны к риску. Они максимизируют налоговые сборы, за исключением стоимости проверки, не учитывая наказание за взятки, но принимая во внимание штрафы за сокрытие дохода.
Так как наивные налоговые инспектора отрицают возможность взяток, то, согласно предположению 7, они максимизируют
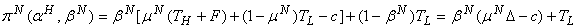 (19)
(19)
где mN - вероятность сокрытия высокого дохода, если исключается возможность взяток. Другими словами, байесовская вероятность равна
mN=aHq/(aHq+1-q) (21)
Опытные налоговые инспектора сталкиваются с более сложной проблемой, так как понимают, что каждый нечестный неплательщик действует согласно наилучшей для него стратегии при объявлении своего дохода. Пусть aD(KT) - вероятность того, что нечестный неплательщик, для которого наказание за взятку составляет KT, скрывает свой высокий доход.
Пусть aH - вероятность того, что честный неплательщик скрывает свой доход. В таком случае опытный налоговый инспектор максимизирует следующую функцию:
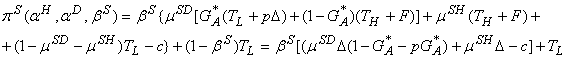 (21)
(21)
где mSD и mSH - вероятности того, что отчет о низком доходе придет от нечестного и честного неплательщиков соответственно. Последние можно найти, используя байесовский подход.
Определение 4.
Для наивного налогового инспектора наилучшим ответом, обозначенным YN(aH), является величина bN, максимизирующая pN(aH,bN). Наилучшим ответом для опытной налоговой инспекции, обозначенным YN(aH, aD), является величина bS, максимизирующая pS(aH, aD,bS).
Следующее утверждение следует из линейности jN по aH и jS по mSH и mD.
Утверждение 3.
Наилучшим ответом для наивного налогового инспектора является
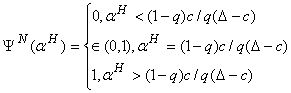 (22)
(22)
Наилучшим ответом опытного налогового инспектора является
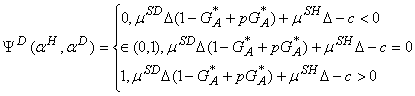 (23)
(23)
где mSH и mD определены выше.
3.3.1 Равновесие в модели коррупции в налоговых органах.
Выше рассматривались два вида налоговых инспекторов: наивные и опытные. Для каждого из этих видов введем понятия равновесия.
Определение 5.
"Наивным" равновесием называется пара (`aH, `bN) такая, что `aH=jH(`bN) и `bN =YN (`aH). "Опытным" равновесием называется тройка.
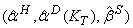 такая, что
такая, что 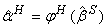 ,
, 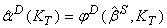 и
и 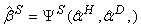 ,
,
Существование единственного наивного равновесия следует из тех же рассуждений, что существование равновесия в модели GRW.
Утверждение 4.
Следует единственное "наивное" равновесие. Это равновесие бывает двух типов
1. Если c > qD, тогда `aH = 1 и `bN=0. Соответствующее этому равновесию значение aD равно единице.
2. Если c £ qD, тогда `aH = (1-q)c/q(D-c) и `bN=(TH-TL)/D º bH. Соответствующее этому равновесию значение aD равно единице.
"Наивное" равновесие первого типа реализуется при высокой цене аудита. В этом случае финансовые проверки не проводятся вообще, и обе категории налогоплательщиков - честные и нечестные - скрывают свой высокий доход. "Наивное" равновесие второго типа реализуется при небольшой цене проверки. В этом случае решение о проведении проверки случайное, как и решение честных неплательщиков скрыть доход. В таком равновесии нечестные неплательщики всегда скрывают свой высокий доход.
В "опытном" равновесии существуют как два описанных выше случая, так и еще два случая, в которых 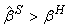 . Эти дополнительные равновесия характеризуются тем, что некоторые нечестные налогоплательщики всегда скрывают доход, а некоторые всегда сообщают о своем высоком доходе. Существует только один вид безразличных нечестных неплательщиков; наказание за взятку для этого типа определим как
. Эти дополнительные равновесия характеризуются тем, что некоторые нечестные налогоплательщики всегда скрывают доход, а некоторые всегда сообщают о своем высоком доходе. Существует только один вид безразличных нечестных неплательщиков; наказание за взятку для этого типа определим как 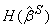 . Используя jD(b;KT), из утверждения 1 получаем
. Используя jD(b;KT), из утверждения 1 получаем
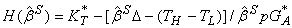 (24)
(24)
Утверждение 5.
Существует единственное "опытное" равновесие. Это равновесие бывает четырех типов:
§ Если 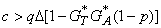 , тогда
, тогда 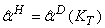 для всех
для всех 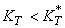 и
и 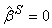 ;
;