Коррупция как объект матеметического моделирования
Страница 12
Пусть цена первоначальной ренты равна 1, а р - ее доля, потраченная на приобретение ренты.
Общие затраты, сделанные участниками на уровне i, равны
ri = pi(1-a1 )(1-a2 )…(1-ai-1 ), i=1,2,…,n (27)
Эти затраты делятся на те, что передаются на следующий уровень:
ti = pi(1-a1 )(1-a2 )…(1-ai ) (28)
и на те, которые потрачены на материальные ресурсы
wi = pi(1-a1 )(1-a2 )…(1-ai-1 ) ai=ri - ti (29)
Тогда общественные издержки конкурентностн первоначальной ренты могут быть подсчитаны как
 (30)
(30)
При совершенной конкуренции, т.е. когда р = 1, и полагая ai = a, получим:
 (31)
(31)
что означает полную растрату ренты при n®¥. При конечном n полная растрата происходит на последнем уровне иерархия.
Если существует барьер для входа нового участника в соревнование за позицию, то р < 1. Возникает соревнование с малым числом участников m, каждый из которых выбирает свои затраты в соответствии с равновесием по Нэшу. В отличие от случая совершенной конкуренции полной растраты ренты здесь не происходит.
Из модели следует, что если при соревновании за ренту используются материальные ресурсы и взятки, а позиции получателей взяток конкурентны, то возникающая структура бюрократии скорее всего будет многоуровневой, а не одно уровневой. Из расчетов по модели также следует, что как в случае совершенной конкуренции, так и конкуренции с небольшим числом участников с ростом числа уровней иерархии повышаются общественные издержки. Данный результат подкрепляет предложения ряда экономистов конституционно закрепить ограничение численности и структуры правительственных организаций.
4.2 Борьба с коррупцией в бюрократии с иерархической структурой.
В ряде работ изучаются модели механизма внутренней коррупции, возникающей в иерархически организованной бюрократии, в которую извне поступают взятки. В такой бюрократии вышестоящие бюрократы должны следить за нижестоящими для предотвращения коррупции. В рамках схемы "хозяин - исполнитель" это означает, что исполнителем является иерархическая организованная бюрократия; ее членов далее будем именовать просто исполнителями. Хозяин назначает "правила игры", а исполнители играют в нее, преследуя при этом (по возможности) свои собственные цели. Ф. Коффман и Дж. Лавари [66] исследовали оптимальную мотивационную схему в двухуровневой организации при наличии возможности сделки между начальником (контролером, supervisor) и подчиненным (исполнителем) и отсутствием (хотя и ценой дополнительных затрат) такой возможности. Результатом работы является вывод, согласно которому коррупция в организации может присутствовать даже в оптимальном состояния.
Развитием этих исследований явилась работа М. Бека [67], где вводится третий исполнитель, который может быть либо средним звеном "вертикальной" иерархии, либо еще одним исполнителем - подчиненным в "плоской" иерархии (см. рис. 1).
Рис. 1. Виды иерархии: а) "вертикальная" h1; б) "плоская" h2
В работе [67] предполагается, что каждому исполнителю (бюрократу) любого уровня иерархии извне предлагается взятка. Бюрократ может ее взять или отказаться. Уровнем "внешней" коррупции считается число бюрократов иерархии, берущих извне взятки. Кроме того, нижестоящие бюрократы могут подкупать вышестоящих бюрократов (в этом случае имеет место внутренняя коррупция в организации). Цель хозяина - минимизация средств, затраченных на достижение некоторого заданного уровня "внешней" коррупции организации. В такой системе исследуется, какова оптимальная форма иерархической структуры и мотивационная схема для бюрократов при наличии в организации внутренней коррупции и при ее отсутствии.
4.2.1 Основные положения и краткое описание модели.
В модели фигурируют четыре участника: хозяин и три исполнителя (i= 1, 2, 3). Эти участники характеризуются следующими параметрами: wi — зарплата исполнителя i; w - гарантированная зарплата исполнителей; z - взятка, которой исполнитель может быть подкуплен (внешняя константа); bi Î [0, 1] - решение о принятии взятки исполнителем i (bi = 1 при принятии, иначе bi = 0). Общий уровень "внешней" коррупции в организации определяется как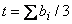 . Хозяин должен разработать иерархическую управленческую структуру, чтобы достичь некоторого уровня "внешней" коррупции. Пусть H = {h1,h2} - множество возможных структур организаций, где h1 - "вертикальная" и h2 - "плоская" иерархии (см. рис. 1); с(nm) - издержки по управлению, где m - уровень усилий по управлению одним подчиненным, n = 1, 2 - число подчиненных. Вероятность m(nm, n) обнаружения факта взяточничества увеличивается с ростом уровня усилий по уравнению. (Предполагается, что c(nm) возрастает и является строго выпуклой, а m(nm, n) возрастает и является строго вогнутой по m, и m(nm, n) ® 1 при m®¥. Кроме того, c(0) = m(0, n) = 0, и m’(nm, n) ® 0 при m ® 0.) За выявление сделки контролеру i выплачивается денежная награда pi. Если исполнитель i - начальник высшего уровня и управляет своими подчиненными с одинаковым уровнем усилий mi, то его ожидаемая прибыль равна Ri(n,pi,t) = pim(nm, n)Sjbj, где Sjbj – ожидаемое число подкупленных подчиненных, а t - целевой уровень коррупции. Цель хозяина — минимизировать издержки, равные сумме зарплат и выплачиваемых наград, при достижении уровня коррупции t. Для достижения этой цели он выбирает награды {pi}, зарплаты {Wj} и иерархию n. Предполагается, что каждый исполнитель i обладает своей функцией полезности Ui(mi,bi), причем все исполнители нейтральны к риску. Поэтому каждый исполнитель выбирает оптимальный для себя уровень усилий и решает, брать ли ему "внешнюю" взятку или нет, исходя из стремления максимизировать EUi(mi,bi) (E - знак математического ожидания). Функция полезности исполнителя представляет собой прибыль, складывающуюся из зарплаты, наград, взяток извне и возможных взяток со стороны подчиненных, за вычетом издержек по управлению подчиненными. Итак, задача хозяина выглядит так
. Хозяин должен разработать иерархическую управленческую структуру, чтобы достичь некоторого уровня "внешней" коррупции. Пусть H = {h1,h2} - множество возможных структур организаций, где h1 - "вертикальная" и h2 - "плоская" иерархии (см. рис. 1); с(nm) - издержки по управлению, где m - уровень усилий по управлению одним подчиненным, n = 1, 2 - число подчиненных. Вероятность m(nm, n) обнаружения факта взяточничества увеличивается с ростом уровня усилий по уравнению. (Предполагается, что c(nm) возрастает и является строго выпуклой, а m(nm, n) возрастает и является строго вогнутой по m, и m(nm, n) ® 1 при m®¥. Кроме того, c(0) = m(0, n) = 0, и m’(nm, n) ® 0 при m ® 0.) За выявление сделки контролеру i выплачивается денежная награда pi. Если исполнитель i - начальник высшего уровня и управляет своими подчиненными с одинаковым уровнем усилий mi, то его ожидаемая прибыль равна Ri(n,pi,t) = pim(nm, n)Sjbj, где Sjbj – ожидаемое число подкупленных подчиненных, а t - целевой уровень коррупции. Цель хозяина — минимизировать издержки, равные сумме зарплат и выплачиваемых наград, при достижении уровня коррупции t. Для достижения этой цели он выбирает награды {pi}, зарплаты {Wj} и иерархию n. Предполагается, что каждый исполнитель i обладает своей функцией полезности Ui(mi,bi), причем все исполнители нейтральны к риску. Поэтому каждый исполнитель выбирает оптимальный для себя уровень усилий и решает, брать ли ему "внешнюю" взятку или нет, исходя из стремления максимизировать EUi(mi,bi) (E - знак математического ожидания). Функция полезности исполнителя представляет собой прибыль, складывающуюся из зарплаты, наград, взяток извне и возможных взяток со стороны подчиненных, за вычетом издержек по управлению подчиненными. Итак, задача хозяина выглядит так
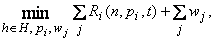 (32)
(32)
при ограничениях
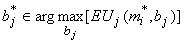 (33)
(33)
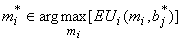 (34)
(34)
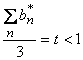 (35)
(35)
EUi ³ w, i = 1,2,3 (36)
NCi(h,pi,wj,t) ³ 0 (37)
где (37) - условие отсутствия внутренней коррупции между начальником i и его подчиненными, и оно может быть включено в число ограничений, а может - и нет.
Вектор (h,pi,wj) - решение этой экстремальной задачи - порождает игру между начальниками и подчиненными. Равновесными стратегиями по Нэшу в этой игре являются векторы (m*j,b*j) (см. ограничения (33), (34)). Ограничение (35) - это условие достижения среднего ожидаемого уровня коррупции, а ограничения (36) - требования, чтобы решение (h*,p*i,w*j) удовлетворяло условию участия исполнителей в игре.
Эта модель анализируется в рамках классической модели "хозяин - исполнитель" с иерархиями H1 и H2. В работе исследуются следующие основные вопросы:
1. может ли хозяин достичь двойной цели - сократить внешнюю коррупцию до заданного уровня без риска одновременно увеличить внутреннюю коррупцию;
2. как форма иерархии минимизирует прибыль ее членов от внутренней коррупции;
3. какая форма иерархии предпочтительнее с точки зрения хозяина.
4.2.2 ОСНОВНЫЕ ВЫВОДЫ
1. Снижение уровня внешней коррупции может привести к тому, что в организации возрастет внутренняя коррупция, т.е. ответ на первый вопрос, вообще говоря, отрицательный.