Коррупция как объект матеметического моделирования

Страница 14

В заключение части 5 настоящего обзора приводятся работы, в которых показы­вается. что систематически повторяющиеся нарушения закона могут превратиться из артефактов в традицию [76], а бороться с аргументами значительно легче, чем с традиционным поведением общества [76,77].

5.1 Модель ограничения коррупции.

Более подробно рассмотрим динамическую модель Ф.Т. Лун [78], представляющую собой простую модель с перекрывающимися поколениями. Она позволяет объяснить, почему, например, уровень коррупции в стра­не может серьезно возрасти по сравнению с некими периодами в прошлом, в то время как параметры схемы наказания не слишком изменились. С другой стороны, она объ­ясняет, почему в сильно коррумпированном обществе обычные мероприятия по борьбе с коррупцией, например усиленные меры слежки за бюрократами, являются дорого­стоящим "удовольствием"' для общества, несопоставимым по сравнению с эффектом от них.

5.1.1 Краткое описание модели и выводы.

В экономике в каждый период существуют два перекрывающихся поколения бюрократов - молодое и старое. Число бюрократов в двух поколениях одинаковое. В каждый период каждому бюрократу предлагается единица дохода в виде взятки, и он решает, принимать ее или нет. Если молодой бюрократ принимает взятку, и его впоследствии проверяют, то с вероятностью единица он должен заплатить денежный штраф в C единиц. Он может продолжить свою работу в следующий период. Однако если он снова возьмет взятку и будет пойман, то новый штраф будет равен уже С' единиц. При этом С' настолько велик, что бюрократ, наказанный еще молодым, не будет принимать другой взятки, пока вероятность проверки положительная величина. Вероятность p(t) проверки бюрократа во время t одинакова для каждого.

Бюрократы в одном поколении различаются только по степеням их честности h. Если бюрократ с честностью h принимает взятку, то он просто оценивает ее в 1 - h единицу. Предполагается, что h - случайная величина с равномерной функцией распределения F(h), h Î [0; 1/f]. Функция распределения F(h) - одинаковая для каждо­го поколения. Предполагается также, что все бюрократы нейтрально относятся к риску.

Во время t старый бюрократ, который раньше не был наказан, примет взятку тогда и только тогда, когда его ожидаемая прибыль составит

1-h-p(t)C ³0 (38)

Пусть W0(t) = 1 - p(t)C. Старый бюрократ с честностью h принадлежит к группе, которая будет коррумпирована тогда и только тогда, когда

W0(t) ³ h (39)

Во время t молодой бюрократ должен принимать во внимание ожидаемую прибыль, когда он станет старым в период t + 1. Пусть вероятность проверки в момент t+1, ожидаемая в t, есть pe(t + 1). Далее, так как наказанный молодой бюрократ в действи­тельности потеряет возможность принять взятку в будущем, молодой бюрократ с честностью h во время t примет взятку тогда и только тогда, когда

1 – h - p(t)[c + max[1 – h - pe(t + 1)c, 0]] ³ 0 (40)

Так как max[1 - h - pe (t + 1)С,0] ³ 0, то возможная стоимость взятки для молодого бюрократа не больше, чем у старого бюрократа. Это говорит о том, что последний более чувствителен к коррупции, чем молодой, поскольку старого бюрократа раньше не наказывали.

ПустьW0(t + 1) = 1 – pe(t + 1)C. Молодой бюрократе честностью h в t предполагает, что он примет взятку в t + 1 тогда и только тогда, когда

W0(t + 1) ³ h (41)

Если (41) удовлетворено,то (40) эквивалентно

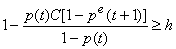(42)

Введем обозначение:

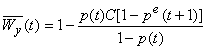(43)

Молодой бюрократ с честностью h примет взятку тогда и только тогда, когда

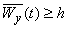(44)

Если (41) не удовлетворено, то молодой бюрократ в t не предполагает принимать взятку в период t + 1. Тогда (40) эквивалентно 1 – h – p(t)C ³ 0.

Пусть Wy(t) = 1 - p(t)C. Молодой бюрократ с честностью h примет взятку тогда и только тогда, когда

Wy(t) ³ h (45)

При этом 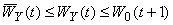тогда и только тогда, когда p(t) > pe(t +1). Доказывается, что при p(t) > pe(t +1) доля молодых коррумпированных бюрократов в t задается функцией 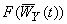, а при p(t) £ pe(t +1) доля молодых коррумпированных бюрократов в t задается 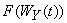. Предполагается, что pe(t) ³ p(t - 1) тогда и только тогда, когда p(t) ³ p(t - 1), другими словами, предположение относительно ожидаемого изменения вероятности проверки оказывается верным. Доказывается, что при pe(t) ³ p(t - 1) пропорция страха коррумпированных бюрократов в t задается (1 - р)(t - 1)F(W0(t)), а при pe(t) < p(t- 1) пропорция старых коррумпированных бюрократов в t задается .

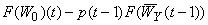Пусть B(t) - доля коррумпированных среди всех бюрократов поколения в момент времени t. B(t) является средним арифметическим между долями старых и молодых коррумпированных бюрократов, которые принимают взятки в момент t. Эта величина используется для измерения уровня коррупции в экономике в момент времени t. Предыдущие результаты могут быть представлены следующими четырьмя случаями:

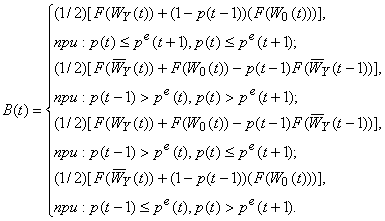(46)

Если все пропорции F(•) меньше единицы, то соответствующие выражения для значений W можно подставить в выражения (46). Тогда получим

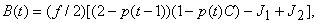(47)

где функции J1 и J2 зависят от p(t - 1), p(t), С, pe(t), pe(t + 1). Из (47) следует, что B(t) зависит от вероятностей проверки, которые определяются ниже.

При более высоком B(t) издержки на эффективную проверку выше. Для включения этого обстоятельства в модель делаются следующие предположения.

Каждый период правительство тратит R единиц ресурсов на проверку. Ресурсы, не­обходимые для эффективной проверки одного человека в момент времени t, есть r(t). Предполагается, что

r(t) = 1/(m-nB(t)), где m > n > 0. (48)

Пусть N - общее число бюрократов. Тогда

p(t) = А – kB(t), где A = Rm/N, k=Rn/N. (49)

Подставляя (49) в (47), можно получить закономерность изменения B(t). Сделанные предположения позволяют показать, что, задавая R, можно получить несколько устой­чивых равновесных уровней коррупции. Пусть первоначальный уровень коррупции в экономике мал. Из-за небольших издержек на проверку каждого человека, R может быть потрачено на большее количество людей. Следовательно, меньше людей выбе­рут стать коррумпированными. Аналогично и в обратном случае при высоком перво­начальном уровне коррупции.

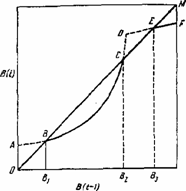
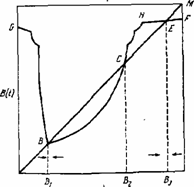
Рис. 2. Фазовая диаграмма Рис. 3. Фазовая диаграмма

Предполагается также, что 1 > A > k >0, C > 1 > AC, f > 1. Как показано в [78], существует три стационарных, равновесных уровня коррупции В* = B(t) для всех t. Вследствие (48), p(t) = р* для всех t, где р* - вероятность про­верки, соответствующая В*. Стационарные уровни возможны только тогда, когда p(t) £ pe(t+1) и p(t-1) £ pe(t). Именно этот случай рассматривается ниже. Поскольку F(WY(t)) = F(W0(t)) =f(1 -p(t))C, если f(1-p(t))C £ 1, и F(WY(t)) = F(W0(t)) = 1, если f(1-р(t)С)>1,то

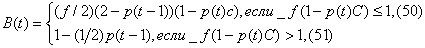
Решение можно представить на фазовой диаграмме. На рис. 2 изображена диа­грамма изменения B(t) от В(t - 1). Кривая ABCD соответствует (50). Она пересекает линию ОМ (эта линия имеет наклон 45%) в двух точках, B и С. Прямая DF, пред­ставляющая уравнение (51), пересекает линию ОМ в точке Е. Таким образом, сущест­вует три точки равновесия и легко может быть показано, что только в точках В и Е оно является устойчивым.

Если изменить предположение о соотношении вероятностей проверки и их ожидае­мых значениях, то, как показано в [78] (с помощью численного моделирования), вместо рис. 2 получаем рис. 3. Из рисунка видно, что если первоначальное значение переменной B(t - 1) больше, чем В2, или если В(t - 1) настолько мало, что B(t) выше точки С, то B(t) сойдется к точке Е. В других случаях B(t) сойдется к точке В.