Коррупция как объект матеметического моделирования
Страница 17
Рис. 4. Выигрыши одного шага игры: I - все h; II - хотя бы одна с.
известны выбранные стратегии и прибыли. Матрица выигрышей одного шага игры изображена на рис. 4. Также всем становится очевиден результат каждого раунда. В каждой суперигре игрок может выбирать между несколькими стратегиями поведения S - коррумпированным и честным. Коррумпированная стратегия С предполагает выбор поведения с на каждом шаге игры. Честная стратегия Н состоит из выбора поведения h на первом шаге суперигры и поведения с в случае, если хоть один из оппонентов выбрал поведение с на предыдущем шаге. Есть два типа игроков - игроки оппортунистического типа, которые могут изменять свою стратегию (их большинство), и игроки, выбирающие стратегию раз и навсегда. Среди таких игроков есть маленькая доля тех, которые всегда выбирают - быть честными в начале каждой новой суперигры.
Стратегия оппортунистического игрока меняется как pst+1 = Zf(ust)pst где рst - пропорция оппортунистических игроков, которые выбрали стратегию s в суперигре, начавшейся во время t, ust - ожидаемая прибыль от выбора стратегии s, а Z - нормализующий фактор, не зависящий от s.
Предполагается также, что прибыли от игры медленно изменяются со временем, а именно происходит убывание, эрозия всех прибылей. Прибыли a, b, с, d удовлетворяют условиям b > а > d > с. Для простоты предполагается, что с равно нулю.
Пропорции игроков с различными стратегиями обозначаются: pH = mH / P - всегда честные; pC = mC / P - всегда коррумпированные; pHt = nHt / P - честные оппортунисты; pCt = nCt / Р - коррумпированные оппортунисты, вычисляемые как число соответствующих игроков по отношению к общему числу игроков. Число оппортунистов принимается за N. Поскольку суперигра осуществляется со случайно выбранными оппонентами, вероятность сыграть против n - 1 относительно честного игрока равна (pHt + pHt)n-1, a вероятность наткнуться хотя бы на одного нечестного – (1 - (pHt + pHt)n-1). В каждой суперигре ожидаемая прибыль от стратегий складывается из общих прибылей каждого шага; соответственно вычислить значения uHt и uCt и получить значение фактора нормализации Z. Обозначим pHt как рt для простоты и, следовательно, pCt за (N/P) - pt получаем главное уравнение эволюции во времени доли оппортунистически честных игроков
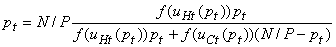 (58)
(58)
где
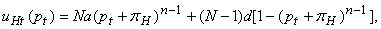 (59)
(59)
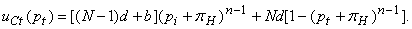 (60)
(60)
Из этого уравнения легко получить условие равновесия
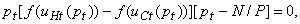 (61)
(61)
т.е. существуют три равновесия:
1. pt = 0;
2. pi = N / P;
3. f(uHt(pt)) = f(uCt(pt)), что означает uHt(pt) = uCt(pt) в силу монотонного возрастания функции f.
(1) соответствует выбору коррумпированного поведения в каждой суперигре, (2) -выбору честного поведения, (3) -случаю, когда относительные выгоды честного и коррумпированного поведения будут одинаковыми. Такое равновесие существует при наличии очень малого числа всегда честных игроков (назовем это первым режимом системы) и отсутствует при наличии значительного числа честных игроков (назовем это вторым режимом системы). Эти две ситуации разделяются условием:
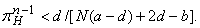
При исследовании стабильности состояний равновесия получено при трех режимах:
при первом режиме равновесие (1) стабильно, но оно перестает таковым быть при втором режиме. Равновесие (2) стабильно при обоих режимах, а равновесие (3), существующее только при первом режиме, является нестабильным.
При включении эффекта эрозии (аt = а - et, bt = b - et, dt = d - et) предполагается, что e достаточно мало, так что ситуация "дилеммы заключенного" всегда сохраняется. Критическое время перехода от первого ко второму режиму при сделанном выше предположении будет иметь порядок 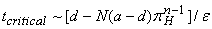 . Таким образом, при достижении некоторого времени система переходит из одного состояния равновесия в другое, т.е. происходит "революция честности". Для возможности такого перехода важное значение имеет наличие в системе хотя бы очень малого процента игроков, всегда выбирающих честную стратегию.
. Таким образом, при достижении некоторого времени система переходит из одного состояния равновесия в другое, т.е. происходит "революция честности". Для возможности такого перехода важное значение имеет наличие в системе хотя бы очень малого процента игроков, всегда выбирающих честную стратегию.
5.4.2 Основные выводы.
В работе [80] показывается, что соединение присутствия малой группы "честных" игроков и совокупных социальных издержек может оказаться достаточно значительным, чтобы привести систему к критической (т.е. катастрофической) точке, в которой устойчивый равновесный уровень коррупции вдруг становится неустойчивым. Когда система находится в такой катастрофической точке, малейшего толчка бывает достаточно, чтобы сместить ее к другому состоянию равновесия. Подобным образом происходит "революция честности". В новом кооперативном состоянии равновесия все игроки выбирают - быть относительно честными, и это равновесие всегда будет устойчивым по условиям модели. Такой катастрофический прыжок в новое равновесие служит примером внезапных и спонтанных мотивов кооперативных шаблонов поведения.
6. ЗАКЛЮЧЕНИЕ
Рынок коррупционных благ, о которых шла речь выше, можно представить в рамках моделей экономического равновесия с двумя видами цен и соответственно двумя рынками - "белым" и "черным". Благами, которыми торгуют на обоих рынках, являются предметы коррупционных сделок (лицензии, налоги и т.п.). На первом, "белом" - легальном, цены фиксированы и блага будут дефицитными. На втором, "черном" - теневом, те же блага распространяются по "рыночным" ценам, "по закону спроса и предложения", который определяет величину "цены", т.е. взятки. Теневой характер второго рынка предопределяет возможность наказания участников. совершающих сделки на этом рынке.
Дефицитность благ вызвана обычными экономическими механизмами согласования при негибких ценах: квотами, очередями, отсутствием информации и времени на ее приобретение. Эти механизмы могут быть естественным следствием регулирования такой экономики либо искусственно созданы теми, кто извлекает выгоду из существования второго - теневого рынка. Число участников такой экономической системы, типы коррупционных благ, правила игры могут меняться со временем экзогенно либо эндогенно. Конкуренция в такой экономике может быть монополистической, олигополитической или даже совершенной. Модель экономики может быть детерминированной либо стохастической, статической либо динамической, а коррупционные блага - товарами дискретными, или делимыми. Именно такой подход позволяет использовать инструментарий общей теории равновесия и, в частности, исследовать вопросы равновесии в такой экономике, их эффективность, а также сравнительную динамику при различных экзогенных параметрах, определяющих, в частности, наказание участников теневого рынка. Разработка таких моделей коррупционных рынков, на наш взгляд, позволит перейти от многочисленных и достаточно фрагментарных моделей коррупции к обобщающей теории коррупции как крупного экономического явления.
Исследование экономики коррупции должно включать в себя также следующее.
§ Сбор, обработку и анализ статистических данных о видах коррупционной активности, областях ее деятельности, мерах борьбы и их фактической результативности.
§ Изучение возможности замены коррупционных актов нормальными с точки зрения и экономики, и юриспруденции контрактами.
§ Разработка экономических институтов и правил, способствующих снижению коррупционной деятельности и уменьшению вероятности ее распространения.
§ Изучение и принятие мер по сокращению коррупции политических деятелей, ответственных за законотворчество в области экономики и управления государственной деятельностью.
Анализ коррупции как социально-экономического и политического явления мог бы базироваться на системе показателей - характеристик различных сторон коррупционной деятельности. На основе этих показателей может быть создана классификация коррупционных сделок. Вот пример такой системы, которая нам представляется целесообразной.