Расчет средней доходности, прогнозирование затрат на привлеченные и размещенные средства, моделирование оптимального привлечения и размещения средств
Страница 2
Предположим, что имеется некоторая зависимость:
Таблица 3
|
x |
x1 |
x2 |
. |
xn |
|
y |
y1 |
y2 |
. |
yn |
, где х - объем привлеченных средств, а у - затраты.
Тогда получатся зависимость:
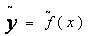 (2)
(2)
В такой постановке задача весьма неопределенна; необходимо указать узкий класс функций.
Таблица 4
Простейшие необходимые условия для наличия эмпирических зависимостей.
|
_
xs |
_
ys |
Вид эмпирической формулы |
Способ выравнивания |
|
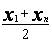
ср. Арифметическое |
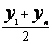
ср. арифметическое |
y=ax+b |
|
|
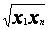
ср. геометрическое |
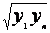
ср. геометрическое |
y=axb |
Y=a+bX, где
X=lgx,
Y=lgy,a=lga |
|
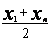
ср. арифметическое |
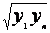
ср. геометрическое |
y=abx или
y=aebx, где
b=lnb |
Y=a+bx, где
Y=lgy, a=lga,
b=lgb |
|
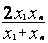
ср. гармоническое |
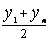
ср. арифметическое |
y=a+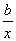 |
Y=ax+b, где
Y=xy |
|
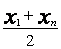
ср. арифметическое |
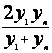
ср. гармоническое |
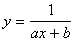
|
Y=ax+b, где
Y=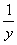 |
|
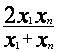
ср. гармоническое |
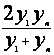
ср. гармоническое |
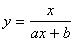
|
Y=ax+b, где
Y=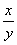 |
|
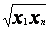
ср. геометрическое |
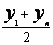
ср. арифметическое |
y=algx+b |
y=aX+b,где
X=lgx |
После построения таблицы 4 для каждого вида формул рассчитываются еще две колонки: 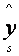 и
и 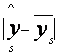 , где
, где
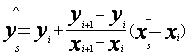 , (3)
, (3)
где xi и xi+1-промежуточные значения, между которыми содержится 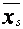
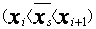
Таблица 5
Схема способа наименьших квадратов.
|
x0 |
x |
x2 |
x3 |
x4 |
y |
xy |
x2y |
|
1 |
x0 |
x02 |
x03 |
x04 |
y0 |
x0 y0 |
x02 y0 |
|
1 |
x1 |
x12 |
x13 |
x14 |
y1 |
x1 y1 |
x12 y1 |
|
1 |
x2 |
x22 |
x23 |
x24 |
y2 |
x2 y2 |
x22 y2 |
|
S0 |
S1 |
S2 |
S3 |
S4 |
t0 |
t1 |
t2 |
Система уравнений для определения коэффициентов:
|
a0s0+a1s1+ .+amsm=t0,
a0s1+a1s2+ .+amsm+1=t1,
a0sm+a1sm+1+ .+ams2m=tm, |
|
(1) |
Решив систему уравнений (1), будем иметь значения коэффициентов а0, а1, а2., и найдем искомый полином:
y=a0+a1x+a2x2, где а0, а1, а2 - известные коэффициенты.
После нахождения эмпирической формулы можно определить значение у для любого х. Найдя формулы зависимости затрат от объема средств легко спрогнозировать их значения в будущие периоды.
Предположим, что затраты увеличиваются по линейной зависимости, тогда
Z = x · yср, где (4)
x - объем привлеченных (распределенных) средств
yср - среднее значение затрат на единицу x
Z - затраты для объема x привлеченных средств.
Так как значение объемов привлеченных (распределенных) средств на будущие периоды на неизвестно, то выразим, для удобства прогнозирования, среднее значение через рост затрат.
Среднее значение затрат на единицу находится по формуле:
yср = (y1-yn)/2, где y1 = b, yn = b+ab(x-1) (5)
y1 - затраты на первую единицу привлеченных (распределенных) средств
yn - затраты на последнюю единицу привлеченных (распределенных) средств
b - затраты на первую единицу привлеченных (распределенных) средств