Моделирование промышленной динамики в условиях переходной экономики
Страница 4
Что можно сказать о постоянной в уравнение? Формально говоря, она показывает прогнозируемый уровень у, когда х=0. Иногда это имеет ясный смысл, иногда нет. Если х=0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам; даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо.
График. Регрессионная зависимость расходов на питание от доходов
(США, 1959-1983гг.)
В данном случае константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике.
При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах. Во-первых, a является лишь оценкой 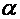 , а b – оценкой
, а b – оценкой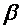 . Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.
. Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.
Интерпретация линейного уравнения регрессии.
Представим простой способ интерпретации коэффициентов линейного уравнения регрессии
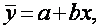
когда у и х – переменные с простыми, естественными единицами измерения.
Во-первых, можно сказать, что увеличение х на одну единицу (в единицах измерения переменной х) приведет к увеличению значения у на b единиц (в единицах измерения переменной у). Вторым шагом является проверка, каковы действительны единицы измерения х и у, и замена слова “единица” фактическим количеством. Третьим шагом является проверка возможности более простого выражения результата, который может оказаться не вполне удобным.
Качество оценки: коэффициент R2
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной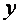 . В любой данной выборке
. В любой данной выборке 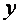 оказывается сравнительно низким в одних наблюдениях и сравнительно высоким – в других. Мы хотим знать, почему это так. Разброс значений
оказывается сравнительно низким в одних наблюдениях и сравнительно высоким – в других. Мы хотим знать, почему это так. Разброс значений 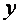 в любой выборке можно суммарно описать с помощью выборочной дисперсии
в любой выборке можно суммарно описать с помощью выборочной дисперсии 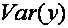 Мы должны рассчитывать величину этой дисперсии.
Мы должны рассчитывать величину этой дисперсии.
В парном регрессионном анализе мы пытаемся объяснить поведение 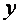 путем определения регрессионной зависимости
путем определения регрессионной зависимости 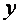 от соответственно выбранной зависимой переменной
от соответственно выбранной зависимой переменной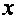 . После построения уравнения регрессии мы можем разбить значение
. После построения уравнения регрессии мы можем разбить значение 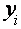 в каждом наблюдении на две составляющих –
в каждом наблюдении на две составляющих –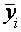 и
и :
:
 (1.5)
(1.5)
Величина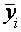 – расчетное значение
– расчетное значение 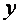 в наблюдении i – это то значение, которое имел бы
в наблюдении i – это то значение, которое имел бы 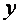 при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина
при условии, что уравнение регрессии было правильным, и отсутствии случайного фактора. Это, иными словами, величина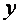 , спрогнозированная по значению
, спрогнозированная по значению 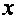 в данном наблюдении. Тогда остаток
в данном наблюдении. Тогда остаток  есть расхождение между фактическим и спрогнозированным значениями величины
есть расхождение между фактическим и спрогнозированным значениями величины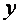 . Это та часть
. Это та часть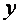 , которую мы не можем объяснить с помощью уравнения регрессии.
, которую мы не можем объяснить с помощью уравнения регрессии.
Используя (1.5), разложим дисперсию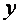 :
:
 (1.6)
(1.6)
Далее, оказывается, что 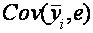 должна быть равна нулю. Следовательно, мы получаем:
должна быть равна нулю. Следовательно, мы получаем:
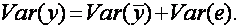 (1.7)
(1.7)
Это означает, что мы можем разложить 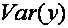 на две части:
на две части: 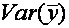 – часть, которая “объясняется” уравнением регрессии в вышеописанном смысле, и
– часть, которая “объясняется” уравнением регрессии в вышеописанном смысле, и 
 – “необъясненную” часть1.
– “необъясненную” часть1.
Согласно (3),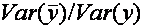 – это часть дисперсии
– это часть дисперсии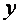 , объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают R2:
, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации, и его обычно обозначают R2:
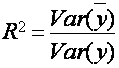 (1.8)
(1.8)
что равносильно
 (1.9)
(1.9)

 Максимальное значение коэффициента
Максимальное значение коэффициента R2 равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что
R2 равно единице. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, так что 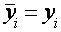 для всех i и все остатки равны нулю. Тогда
для всех i и все остатки равны нулю. Тогда 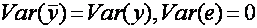 и R2=1.
и R2=1.
Если в выборке отсутствует видимая связь между 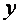 и
и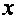 , то коэффициент R2 будет близок к нулю.
, то коэффициент R2 будет близок к нулю.
 При прочих равных условиях желательно, чтобы коэффициент R2 был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов a и b, чтобы максимизировать R2. Не противоречит ли это нашему критерию, в соответствие, с которым a и b должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Что эти критерии эквивалентны, если (1.9) используется как определение коэффициента R2. Отметим сначала, что
При прочих равных условиях желательно, чтобы коэффициент R2 был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов a и b, чтобы максимизировать R2. Не противоречит ли это нашему критерию, в соответствие, с которым a и b должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Что эти критерии эквивалентны, если (1.9) используется как определение коэффициента R2. Отметим сначала, что
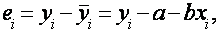 (1.10)
(1.10)
откуда, беря среднее значение ei по выборке и используя уравнение
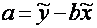 (1.11),
(1.11),
получим: 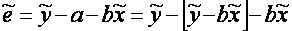 . (1.12)
. (1.12)
Следовательно,
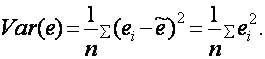 (1.13)
(1.13)
Отсюда следует, что принцип минимизации суммы квадратов остатков эквивалентен минимизации дисперсии остатков при условии выполнения (1.12).
Однако если мы минимизируем 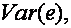 то при этом в соответствии с (1.9) аавтоматически максимизируется коэффициент R2.
то при этом в соответствии с (1.9) аавтоматически максимизируется коэффициент R2.
Альтернативное представление коэффициента R2.
На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, тем больше должен быть коэффициент корреляции для фактических и прогнозных значений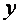 , и наоборот. Покажем, что R2 фактически равен квадрату такого коэффициента корреляции между
, и наоборот. Покажем, что R2 фактически равен квадрату такого коэффициента корреляции между 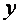 и
и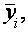 ,который мы обозначим
,который мы обозначим 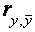 (заметим, что
(заметим, что 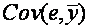 = 0):
= 0):