Моделирование работы банка

Страница 4

III. Общую сумму прибыли, заработанную банком, необходимо перерас­пределить, во-первых, по осуществляемым отдельным операциям и услугам, во-вторых, по функциональным подразделениям. Данный этап интегрирует результаты двух предыдущих и является наиболее трудоемким.

Данная разбивка финансовых результатов может производиться до уровня любой глубины - вплоть до каждого отдельного вида услуг и функционально­го подразделения - филиала или отдела.

Рассмотрим общий случай.

3.2.Постановка задачи.

Некоторый банк, организационная структура которого построена на базе отделений, ежегодно распределяет ассигнования на выполнение различных работ. Каждое из S отделений представляет руководству банка данные трех видов . Информация первой группы относится к проведению поисковых исследований неопределенного характера . Если на исследования такого рода в отделении j выделяют vj тысяч долларов, то оценка ожидаемого долгосрочного дохода равна Pj (vj ) миллионов долларов. Информация второй группы относится к услугам, по которым поисковые исследования уже завершены и для внедрения которых требуется проведение ряда работ и подсчетов. Для таких проектов ассигнования в объеме wj тысяч долларов, согласно имеющейся оценке, дадут, в конечном счете, доход в размере Qj (wj ) миллионов долларов. К третьей группе относится информация , связанная с улучшением качества уже оказываемых услуг . Затраты xj тысяч долларов, согласно сделанным оценкам, должны принести всего Rj(xj) миллионов долларов дополнительного дохода.

Правление банка утверждает общую сумму ассигнований на все проекты в размере N тысяч долларов, и верхний предел Lj ассигнований между отделениями j. Следовательно, необходимо распределить ассигнования между отделениями таким образом, чтобы обеспечивалась максимизация общего дохода банка при наложенных ограничениях.

Математическая модель задачи описывается следующими соотношениями:

[Pj (v j ) + Q j (w j ) + Rj (x j )] (1)

максимизировать, при ограничениях

(vj + wj + xj ) 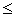N (2)

общая сумма ассигнований

vj + wj + xj 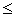Lj , j=1,2 s (3)

vj , wj , xj (4) неотрицательные целые при любом j .

Поскольку на все управляемые переменные наложено только одно ограничение (2) , а остальные бюджетные и целочисленные ограничения (3) и (4) относятся только к отделению j ,то в данном случае имеет место задача распределения усилий с одним ограничением.[3] Таким образом получаем следующее рекуррентное соотношение :

gj (n) = max [ Pj ( vj ) + Qj (wj ) + Rj (xj ) + gj ( n - vj - wj - xj ) ] , j = 1,2 .s (5)

где n = 0,1,2 .N и максимизация производится только по неотрицательным целочисленным значениям vj ,wj и xj удовлетворяющим условию:

vj + wj + xj 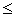min (Lj , n)

На каждом шаге отыскания максимума можно использовать метод решения задачи о распределении усилий, представив этот пример в следующем виде:

Pj ( vj ) + Qj (wj ) + Rj (xj ) 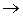max (6) при ограничениях

vj + wj + xj 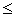y , (7)

где vj ,wj и xj должны быть неотрицательными целыми числами. Необходимо получить решение для каждого значения y = 0,1 Lj .

Чтобы использовать рекуррентный подход к задаче (6)-(7) , примем

p j (y) = Pj (y) , y = 0,1 .Lj , (8)

q j (y) = max [ Qj (wj ) + pj ( y- wj ) ] , y = 0, 1 . Lj (9)

wj

где максимизация производится только по неотрицательным целым значениям

wj 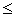y , и

r j (y) = max [ Qj (xj ) + q j (y - xj )] , y = 0,1 . Lj (10)

xj

где максимизация производится только по неотрицательным целым значениям

xj 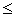y .

Далее находится решение по соотношению:

g j (n) = max [ r j (y) + g j ( n - y ) ] , j = 1,2 .s, (11)

y

где n = 0,1 .N и максимизация производится только по неотрицательным целым значениям y , удовлетворяющим условию у 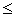min (Lj , n) .

Следовательно, для решения этой задачи нужно связать s расчетов распределения усилий с общей моделью распределения усилий.

Таким образом, в качестве решения мы получим значения vj , wj и xj - выделяемые средства на соответствующие проекты, дающие максимизацию общего дохода банка g j (n) по отделам j = 1,2 .s .

Заключение.

Коммерческий банк - это кредитное учреждение, реализующее экономические интересы. Банковское дело - как правило, весьма выгодный бизнес, основанный на определенных принципах. Основной - прибыльность. Показатель прибыли официально считается основным показателем деятельности банка. Иначе говоря, размер капитала, т.к. в балансовом отчете в разделе собственные средства (капитал) прибыль занимает не последнее место. Размер капитала банка имеет исключительное значение для его деятельности. Во-первых, регулирующие органы устанавливают мини­мально необходимый размер капитала для вновь созда­ваемых и работающих банков. Во-вторых, капитал бан­ков служит основой (капитальной базой) для установ­ления регулирующими органами нормативов, определя­ющих контролируемые показатели их деятельности. Наконец, чем больше размер капитала банка, тем выше уверенность его вкладчиков, кредиторов и клиентов, поскольку при этом повышается его надежность.

Т.о. для получения наибольшей прибыли предполагается создание и организация:

системы информации;

системы прогнозирования денежных ресурсов;

системы принятия решений;

системы контроля.

Приложение.

Модель общего вида задачи распределения усилий.

Такой же динамический под­ход в той же мере справедлив и в случае, когда огра­ничение нелинейно, и в случае, когда огра­ничение является линейным.

Модель описывается следующими соотношениями:

Максимизировать (1’)

при ограничениях (2’)

yj = 0 , 1, 2, . при любом j. (3’)

Допустим, что каждая функция Hj(yj) есть неубывающая функция, принимающая целочисленные значения при любом yj = 0, 1, 2, . и удовлетворяющая условию Hj(0) = 0. Для упрощения рассужде­ний принимается, что H1(y1) = y1, вследствие чего допустимое решение существует при любом значении N. На каждую величину yj можно также наложить ограничение сверху.

Рекуррентное соотношение динамического программирования, соответствующее задаче (1’) — (3’), имеет следующий вид:

gj = max {Rj (yj) +gj-1 [ n – Hj(yj)]}, j = 1,2, .,s, (4’)

g0 ( n ) ≡ 0, j = 0 , (5’)

где n = 0, 1, ., N, а максимум берется только по неотрицатель­ным целочисленным значениям yj, удовлетворяющим условию Hj(yj) ≤ n. Отыскивается значение gs(N). Для выполнения вычисле­ний нужно определить по выражению (4’) значения каждой функции gj(n) при n = 0, 1, ., N, начиная с j = 1 и заканчивая j=s.

Литература.

1)Банки и банковские операции: Учебник для вузов. / Под редакцией Е.Ф.Жукова.

-М.:Банки и биржи , ЮНИТИ ,1997.

2)Банковское дело / Под редакцией О.И.Лаврушина. М .: Банковский и биржевой научно- консультационный центр , 1992 .

3)Банковское дело / Под редакцией В.И.Колесникова , Л.П.Кроливецкой .- М.:Финансы и статистика , 1995 .