Общая теория статистики

Страница 5

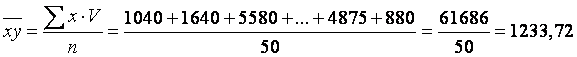
Расчет коэффициента корреляции проведем по первой из предложенных в начале решения двух формул:

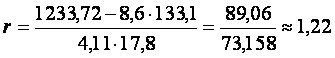
Вывод: т.к. полученный коэффициент корреляции больше значения 0,8, то можно сделать вывод о том, что теснота связи между исследуемыми признаками достаточно тесная.

Задание 7.

По данным своего варианта (см. табл. N) рассчитать индексы сезонности, построить график сезонности и сделать выводы.

Исх. данные:

1) Табл. N

Месяц	Годы	Итого за 3 года	В сред-нем за месяц	Индексы сезон-ности, %
1991	1992	1993
1	2	3	4	5	6	7
Январь	4600	2831	3232	10663	3554	90,3
Февраль	4366	3265	3061	10692	3564	90,6
Март	6003	3501	3532	13036	4345	110,5
Апрель	5102	2886	3350	11338	3779	96,1
Май	4595	3054	3652	11301	3767	95,8
Июнь	6058	3287	3332	12677	4226	107,4
Июль	5588	3744	3383	12715	4238	107,8
Август	4869	4431	3343	12643	4214	107,1
Сентябрь	4065	3886	3116	11067	3689	93,8
Октябрь	4312	3725	3114	11151	3717	94,5
Ноябрь	5161	3582	2807	11550	3850	97,0
Декабрь	6153	3598	3000	12751	4250	108,0
В среднем	5073	3482	3244		3953	100,0

Сезонными колебаниями называют устойчивые внутригодовые колебания в ряду динамики. Они характеризуются индексами сезонности, совокупность которых на графике образует сезонную волну.

Воспользуемся следующей формулой расчета индексов сезонности: