Геоморфология

Страница 3

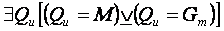, (7)

Здесь 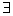(перевернутая буква Е) — квантор существования, читаемый как «существует хотя бы один», 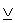— логический союз «или» разделительное, требующий выполнения одного, и только одного из связываемых им высказываний. В целом, условие (7) читается как «существует хотя бы одно такое множество Qu (входящее в систему 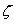множеств, из которых строится пространство состояний W), которое удовлетворяет высказыванию, заключенному в квадратные скобки, представляя собой либо множество M, либо множество Gm».

Множества Gm могут входить как в область значений, так и в область определения соответствия (6). Пусть мы имеем условие:

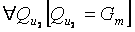(8)

Здесь 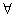(перевернутая буква А) — квантор общности, имеющий смысл слова «все». Выражение (8) читается как «все множества 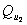должны представлять собой только множества Gm», т.е. областью значений соответствия (6) при соблюдении условия (8) могут быть только те множества, на которых принимают значения геометрические характеристики рельефа. Множества, на которых принимают значения рельефообразующие факторы, элементы пространства и времени, могут входить только в область определения соответствия (6). Иначе говоря, соответствиями, удовлетворяющими условию (8), выражаются зависимости очертаний рельефа от местоположения, времени, рельефообразующих факторов, а также взаимосвязи геометрических характеристик рельефа. Ясно, что установление такого рода соответствий относится к задачам геоморфологии, сюда же отнесем соответствия, удовлетворяющие приводимому ниже условию (10).

В других случаях геометрические характеристики рельефа могут входить в область определения соответствия (6), определяя собой либо значения геологических, гидрологических, биогеографических и прочих факторов, которые в задачах, удовлетворяющих условию (8), рассматривались как рельефообразующие, либо (в геохронологических исследованиях) время. Этим случаям отвечает условие:

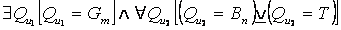, (9)

где 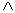— логический союз «и», означающий, что должны выполняться оба связываемые им высказывания. Примерами задач такого рода могут служить: установление зависимости характеристик потока от формы ложа, дешифрование геологического строения по очертаниям рельефа, измерение времени скоростью денудации. Отнесение такого рода задач к геоморфологии или к смежным к ней наукам в той или иной мере условно. Те из задач, которые можно отнести к геоморфологии, мы будем называть ее пограничными задачами. Таким образом, условие (9) является необходимым, но недостаточным точно так же, впрочем, как и условие (8), которому могут удовлетворять пограничные задачи смежных с геоморфологией наук.

В построении пространства состояний рельефа непременно, в явном или неявном виде, должно участвовать множество T элементов времени t. В неявном виде, принимая значения на одноэлементном множестве, оно присутствует, когда изучается состояние рельефа в фиксированный, современный или прошлый момент или промежуток времени. В таких случаях среди рассматриваемого множества элементов времени любые два элемента 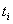и 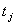совпадают: 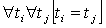. Явно время вводится при изучении развития рельефа. При этом мы, очевидно, должны иметь условие, противоположное предыдущему, а именно: .

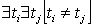В пределах внутренних задач геоморфологии, определяемых условием (8), а также приводимым ниже условием (10), можно либо не учитывать, либо учитывать рельефообразующие факторы. В первом случае имеет место условие 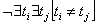, во втором 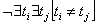. Здесь 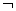— знак логического отрицания «не», который, будучи поставлен перед квантором существования 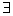, отрицает его, так что 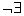означает «не существует».

Накладывая на пространство (5) и соответствия (6) приведенные условия, можно поставить основные задачи геоморфологии и выделить разделы науки, в которых они решаются.

В пределах внутренних задач геоморфологии, т.е. при выполнении условий (8) или (10), логическое обоснование получают четыре раздела геоморфологии — геометрия, статика, кинематика и динамика рельефа, ранее выделявшиеся интуитивно (Девдариани, 1966).

1. Геометрия рельефа:

.

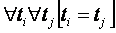Изучаются очертания рельефа в фиксированный момент или промежуток времени. Наиболее часто встречающейся задачей геометрии рельефа является установление соответствий вида 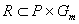, где под P понимается двумерное (карта) или одномерное (профиль) евклидово пространство. В частности, обозначив координаты точки земной поверхности в трехмерном пространстве 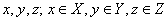, и положив 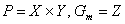, получим соответствие 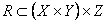, под которым с одинаковым правом можно понимать и карту в горизонталях, и аппроксимирующую ее функцию .

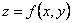Другая задача геометрии рельефа состоит в установлении зависимостей между различными геометрическими характеристиками рельефа, т.е. соответствий вида 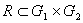. Примером такого соответствия, сформулированного в качественной форме, может служить утверждение, что с возрастанием высоты (принимающей значения на упорядоченном множестве G1) уклоны (принимающие значения на упорядоченном множестве G2) преимущественно (это слово указывает на неоднозначность соответствия, его вероятностный характер) возрастают.

2. Статика рельефа: .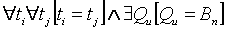

Изучаются зависимости очертаний рельефа от рельефообразующих факторов в фиксированный момент или промежуток времени. Очевидно, что такие зависимости имеют геоморфологический смысл, если рельеф достиг устойчивого равновесия (например, предельного профиля) и более не изменяется во времени.

3. Кинематика рельефа: .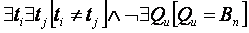

Изучаются изменения состояния рельефа во времени вне зависимости от вызывающих эти изменения рельефообразующих факторов. При этом могут использоваться два метода описания движения: а) Локальный метод, когда объектами наблюдения служат элементы p физического пространства (например, точки на карте), в которых с течением времени t изменяются геометрические характеристики рельефа g1, g2, …, gk. Соответствие (6) получает вид

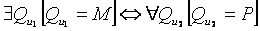. (10)

Здесь знак 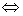обозначает логическое отношение эквивалентности, смысл которого состоит в том, что первое высказывание, утверждающее присутствие в области определения соответствия (6) множества M, требует осуществления второго высказывания, гласящего, что областью значений соответствия является только множество P, и наоборот. Выражение (10) является упоминавшимся выше вторым наряду с (8) условием, определяющим внутренние задачи геоморфологии.