Геоморфология
Страница 4
4. Динамика рельефа: 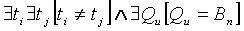 .
.
Изучается развитие рельефа при активном или пассивном воздействии рельефообразующих факторов. Примером в терминах континуальной математики может служить уравнение развития продольного профиля реки: 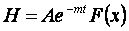 , где H — высота точки профиля, A — постоянная, зависящая от его начальных очертаний; они представляют собой геометрические характеристики рельефа, принимающие значения на множествах G1 и G2 соответственно; t — время, принимающее значения на множестве T; F(x) — функция расстояния x, принимающего значения в одномерном евклидовом пространстве P; m — постоянная, зависящая от рельефообразующих факторов, принимающих значения на множествах B1, B2, …, Bl; e — основание натуральных логарифмов. Все перечисленные характеристики принимают значения из множества действительных чисел, и приведенное уравнение представляет собой конкретную форму функционального соответствия
, где H — высота точки профиля, A — постоянная, зависящая от его начальных очертаний; они представляют собой геометрические характеристики рельефа, принимающие значения на множествах G1 и G2 соответственно; t — время, принимающее значения на множестве T; F(x) — функция расстояния x, принимающего значения в одномерном евклидовом пространстве P; m — постоянная, зависящая от рельефообразующих факторов, принимающих значения на множествах B1, B2, …, Bl; e — основание натуральных логарифмов. Все перечисленные характеристики принимают значения из множества действительных чисел, и приведенное уравнение представляет собой конкретную форму функционального соответствия  в многомерном евклидовом пространстве состояний
в многомерном евклидовом пространстве состояний 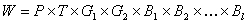
Рассмотрим бесконечную упорядоченную последовательность элементов времени:
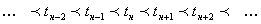
Знак 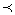 указывает, что стоящий перед ним элемент предшествует элементу, стоящему после. Для элементов множества действительных чисел знак
указывает, что стоящий перед ним элемент предшествует элементу, стоящему после. Для элементов множества действительных чисел знак 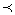 равносилен знаку < (меньше), а
равносилен знаку < (меньше), а 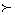 — знаку > (больше). Для элементов времени
— знаку > (больше). Для элементов времени 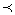 означает раньше, а
означает раньше, а 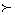 позже. В указанной последовательности важнейшую грань образует момент (или промежуток) времени tн, в который произведены (или начаты) наблюдения за состоянием рассматриваемой системы. Для последующих элементов времени,
позже. В указанной последовательности важнейшую грань образует момент (или промежуток) времени tн, в который произведены (или начаты) наблюдения за состоянием рассматриваемой системы. Для последующих элементов времени, 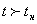 , состояния рельефа определяются методами интерполяции и экстраполяции, а для предыдущих,
, состояния рельефа определяются методами интерполяции и экстраполяции, а для предыдущих, 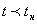 — восстанавливаются историческим и методами, на основании сохранившихся свидетельств прошлых состояний. В соответствии с этим в каждом из разделов геоморфологии следует различать задачи:
— восстанавливаются историческим и методами, на основании сохранившихся свидетельств прошлых состояний. В соответствии с этим в каждом из разделов геоморфологии следует различать задачи:
1) изучения современного и прогнозирование будущего рельефа, определяемые условием 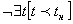 ;
;
2) изучения прошлого рельефа, определяемые в кинематике и динамике рельефа условием 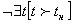 , а в геометрии и статике рельефа — условием
, а в геометрии и статике рельефа — условием  .
.
Пограничные задачи геоморфологии делятся на пограничные задачи геометрии рельефа, когда 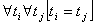 , и пограничные задачи кинематики рельефа, когда
, и пограничные задачи кинематики рельефа, когда 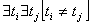 при соблюдении, разумеется условия (9).
при соблюдении, разумеется условия (9).
Использованная литература.
1. Журнал «Геоморфология», А.С. Девдариани, №1, 1971г., с.46-55.
Автором была использована литература:
2. Геология и математика. «Наука», Новосибирск, 1967.
3. Девдариани А.С. Итоги науки. Геоморфология, вып.1. Математические методы. Изд. ВИНИТИ, М., 1966.
4. Косыгин Ю.А., Воронин Ю.А., Соловьев В.А. Опыт формализации некоторых тектонических понятий. Геол. и геофиз., 1964, №1.
5. Косыгин Ю.А., Воронин Ю.А. Геологическое пространство как основа структурных построений. Статья 1. Геол. и геофиз., 1965, №9.
6. Родоман Б.Б. Математические аспекты формализации порайонных географических характеристик. Вестн. МГУ. География, 1967, №2.
7. Стинрод Н., Чинн У. Первые понятия топологии. «Мир», М., 1967.
8. Уитроу Дж. Естественная философия времени. «Прогресс», М., 1965.
9. Шиханович Ю.А. Введение в современную математику. «Наука», М., 1965.
[1] Автор не накладывает никаких ограничений на множества, входящие в прямое произведение W, и допускает, в частности, что они могут быть неупорядоченными. Поэтому множество векторов, образующих W, не является пространством в строгом математическом понимании. Однако автору представляется, что в географических и геологических целях такое расширение математического понятия пространства было бы весьма удобным. И это не шло бы в разрез с общей тенденцией расширения понятия пространства в математике от трехмерного евклидова к многомерным евклидовым, затем к метрическим и далее к топологическим пространствам.