Системы стабилизации и ориентации
Системы стабилизации и ориентации
Реферат
В данном курсовом проекте изучаются методы анализа и синтеза систем стабилизации и возможность применения для этого математического пакета MAPLE V. Разработана библиотека процедур, позволяющая облегчить работу студентов при выполнении курсового проекта по дисциплине «Системы стабилизации и ориентации».
Пояснительная записка содержит 36 листов, 3 приложения и 7 рисунков.
Содержание
Введение
1 Обзор литературы
1.1 Получение дискретной модели непрерывной системы…….
1.2 Передаточные функции непрерывных и дискретных
систем………………………………………………………….
1.3 Частотные характеристики непрерывных и
дискретных систем .…….
1.4 Анализ устойчивости непрерывных и
дискретных систем…… .
1.5 Синтез цифровых систем управления по желаемым
частотным характеристикам разомкнутой системы …
2 Разработка библиотеки процедур в среде Maple
2.1 Получение дискретной модели непрерывной системы
2.1.1 Процедура diskretA
2.1.2 Процедура diskretB
2.2 Получение матрицы передаточных функций………………
2.2.1 Процедура permatr .
2.3 Построение частотных характеристик дискретной и
непрерывной систем………………………………………….
2.3.1 Процедура afch
2.3.2 Процедура lach
2.3.3 Процедура lfch
2.4 Анализ устойчивости дискретной и непрерывной систем
2.4.1 Процедура klark
2.4.2 Процедура gurvitz .
2.4.3 Процедура ust
2.5 Синтез дискретных систем
2.5.1 Процедура sintez1 .
2.5.2 Процедура sintez2 .
3 Апробация библиотеки процедур SSO .
Заключение
Список литературы .
Введение
В настоящее время в промышленности и сельском хозяйстве применяются десятки тысяч систем автоматического регулирования (САР), которые обеспечивают высокую эффективность производственных процессов. Поэтому теория автоматического регулирования изучается во всех высших учебных заведениях в качестве одной из базовых дисциплин. На её основе в дальнейшем читаются такие курсы, как теория автоматического управления, автоматизированные системы переработки информации, управление технологическими и организационно-экономическими процессами, теория автоматизированного проектирования систем и их математическое обеспечение, а также целый ряд дисциплин специального назначения. Объекты и устройства систем регулирования отличаются по своей физической природе и принципам построения, поэтому проектировщику необходимо не только иметь хорошую подготовку в области механики, электроники, электротехники и вычислительной техники, но и уметь учитывать специфические особенности объекта. С целью овладения практическими навыками использования методов теории автоматического регулирования будущие специалисты в процессе обучения выполняют домашние задания, курсовые и дипломные работы по проектированию систем управления конкретными объектами.
Трудность выполнения проектных работ в значительной степени определяется сложностью математического аппарата, используемого при описании объектов и систем автоматического регулирования. Поэтому для облегчения решения задач теории автоматического регулирования имеет смысл создание процедур, реализующих ряд алгоритмов проектирования систем. Они позволяют формировать обобщенные модели элементов в дискретной форме и матрицы передаточных функций; строить амплитудно-фазовые частотные характеристики (в обычном и логарифмическом масштабах) и др.
1 Обзор литературы
1.1 Получение дискретной модели непрерывной системы
При проектировании непрерывных, дискретно-непрерывных и дискретных САР необходимо располагать математической моделью элемента (объекта). При высоких порядках моделей удобно пользоваться уравнениями, составленными во временной области и записанными в векторно-матричной форме. Рассмотрим одну из наиболее часто встречающихся форм представления многоконтурных стационарных линейных элементов (объектов). При этом будем считать, что в линейный объект регулирования после ряда преобразований входят лишь две матрицы: А и В. Тогда эту форму представления стационарного объекта можно записать в виде векторно-матричного уравнения
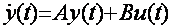 , (1.1)
, (1.1)
где у и u-векторы размерностей (n ´ 1) и (m ´ 1); А и В - матрицы размерности (n´ n) и (n´ m).
С целью использования одинаковой формы описания объектов непрерывных, дискретно-непрерывных и дискретных САР пользуются теорией спектрального разложения матриц, которая с помощью специально созданных алгоритмов позволяет получать единые математические модели в дискретной форме. К основному преимуществу такого подхода следует отнести возможность представления моделей с использованием матриц до 50-80-го порядков, без существенного понижения точности спектрального разложения матриц.
Рассмотрим алгоритмы, с помощью которых составляются дискретные модели многомерных объектов, описываемых типовым векторно-матричным уравнением (1.1). Аналитическое решение этого уравнения при начальных условиях y(t0) имеет вид
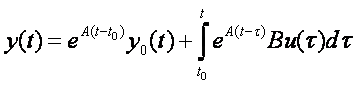 (1.2)
(1.2)
В моменты времени t=кT0 и t=(к+1)Т0 состояние объекта ук+1 связано с предыдущим состоянием ук соотношением
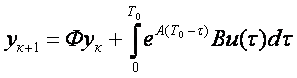 (1.3)
(1.3)
где 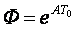 - переходная матрица системы уравнений.
- переходная матрица системы уравнений.
Математические зависимости для алгоритмов дискретных моделей можно составить с тремя типами экстраполяторов.
Самая простая дискретная модель может быть получена, если положить, что внутри интервала квантования сигнала, и (t) экстраполируется по одной точкеступеньки со значениями ик , т.е. перед объектом включен экстраполятор нулевого порядка Э0. В этом случае соотношение (1.3) можно представить в виде
ук+1=Фук+Fик . (1.4)
Здесь F=(Ф - I)А-1В - матрица коэффициентов, обеспечивающих передачу сигналов по входам дискретной модели.
1.2 Передаточные функции непрерывных и дискретных систем
Под передаточной функцией стационарных элементов понимают отношение изображения выходной величины к изображению функции входной величины, полученные при нулевых начальных условиях. Для многоконтурных стационарных элементов возможно получение матрицы передаточных функций на основе модели системы во временной области в векторно-матричной форме (1.1). Применяя преобразование Лапласа, получим:
IX(s)=AX(s)+BU(s), (1.5)
где I - единичная матрица. Путем несложных преобразований найдем:
X(s)=(Is – A)-1BU(s). (1.6)
Таким образом, матрицу передаточных функций в общем виде можно записать так:
MU=X(s)/U(s)=(Is – A)-1B (1.7)
1.3 Частотные характеристики непрерывных и
дискретных систем
Частотные характеристики линейных непрерывных систем находятся из передаточных функций после подстановки в них s=jw и выделения действительной мнимой частей, т.е.
W0(jw)=U0(w)+jV0(w), (1.8)
где U0(w) и V0(w) - соответственно действительная и мнимая частотные характеристики.
Пользуясь выражением (1.8), в декартовой системе координат строят амплитудно-фазовые частотные характеристики W0(jw). Если перейти к полярной системе координат, то выражение (1.8) можно переписать в виде
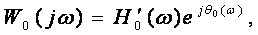 (1.9)
(1.9)
где 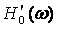 и q0(w) - соответственно амплитудная и фазовая частотные характеристики.
и q0(w) - соответственно амплитудная и фазовая частотные характеристики.