Системы стабилизации и ориентации
Страница 4
x2 - правый предел изменения частоты;
y1 и y2 - границы изменения логарифмической амплитуды.
Описание:
Процедура строит ЛАЧХ дискретной и непрерывной систем согласно методике, описанной в пункте 1.3.
Пример:
lach(1/(4*s^2-1.8*s+2),s,0.1,5,-50,0);
Полученный график можно увидеть на рисунке А.1 приложения А.
2.3.3 Процедура lfch - построение логарифмической фазо-частотной характеристики дискретной и непрерывной систем.
Формат:
lfch(W, c, Т0, x2, y1, y2)
Параметры:
W - передаточная функция системы;
с - строковая переменная s или z, обозначающая АФЧХ какой системы необходимо построить;
Т0 - такт квантования для дискретной системы;
x2 - правый предел изменения частоты;
y1 и y2 - границы изменения логарифмической фазы.
Описание:
Процедура строит ЛФЧХ дискретной и непрерывной систем согласно методике, описанной в пункте 1.3.
Пример:
lfch(1/(4*s^2-1.8*s+2),s,0.1,3,0,Pi);
Полученный график можно увидеть на рисунке Б1 приложения Б.
2.4 Анализ устойчивости
дискретной и непрерывной систем
2.4.1 Процедура klark - построение особых линий для определения области устойчивости дискретных систем.
Формат:
klark(А, В, К, x1, x2, y1, y2)
Параметры:
А - матрица состояния дискретной системы;
В - матрица управления дискретной системы;
К - матрица;
x1 и x2 - пределы изменения параметра к1;
y1 и y2 - пределы изменения параметра к2;
Описание:
Процедура строит особые линии для определения области устойчивости дискретных систем по критерию Кларка, описанному в пункте 1.4. При задании матрицы К необходимо два изменяемых параметра обозначить к1 и к2.
Пример:
Построенный график можно увидеть на рисунке Б.1 приложения Б.
2.4.2 Процедура gurvitz - построение особых линий для определения области устойчивости непрерывных систем.
Формат:
gurvitz(А, В, К, x1, x2, y1, y2)
Параметры:
А - матрица состояния непрерывной системы;
В - матрица управления непрерывной системы;
К - матрица;
x1 и x2 - пределы изменения параметра к1;
y1 и y2 - пределы изменения параметра к2;
Описание:
Процедура строит особые линии для определения области устойчивости непрерывных систем по критерию Гурвица, описанному в пункте 1.4. При задании матрицы К необходимо два изменяемых параметра обозначить к1 и к2.
Пример:
Построенный график можно увидеть на рисунке В.1 приложения В.
2.4.3 Процедура ust - оценивает устойчивость непрерывной и дискретной замкнутых систем.
Формат:
ust(A, B, K, c)
Параметры:
А - матрица состояния непрерывной или дискретной системы;
В - матрица управления непрерывной или дискретной системы;
К - матрица;
с - строковая переменная s или z, которая обозначает устойчивость какой системы необходимо оценить.
Описание:
Процедура оценивает устойчивость непрерывной и дискретной замкнутых систем по корневому критерию.
Процедура возвращает строковую переменную,
принимающую значения:
ust - система устойчива;
noust - система не устойчива;
nagr - система находится на границе устойчивости.
Пример:
ust(matrix(2, 2, [0,1,2.268,-0.03]), matrix(2,1,[0,-4.235]),
matrix(1, 2, [1,0]), z);
noust
2.5 Синтез дискретных систем
2.5.1 Процедура sintez1 - определяет коэффициенты корректи-рующего звена.
Формат:
Sintez1(W, Wg, a, T0)
Параметры:
W - исходная передаточная функция;
Wg - вектор желаемых значений АФЧХ при определенных значениях частоты;
А - вектор значений частоты;
T0 - такт квантования.
Описание:
Процедура возвращает коэффициенты корректирующего звена, реализующего первый закон управления (формула 1.26) по квадратичному критерию (1.23).
Пример:
W := .5*(-93478.39101*z-.1150000000e3*z^2
+902.6600000*z^3+1026.926837)/(z^5-.5570000000*z^4-
124.6542298*z^3+46.10663267*z^2+328.8088091*z-4.226757788)
a:=vector(3,[10,100,1000]): Wg:=vector(3,[1,-1,-4]): Т0:=0.063:
sintez1(W, Wg, a, t0);

2.5.2 Процедура sintez2 - определяет коэффициенты корректи-рующего звена.
Формат:
Sintez1(W, Wg, a, T0)
Параметры:
W - исходная передаточная функция;
Wg - вектор желаемых значений АФЧХ при определенных значениях частоты;
а - вектор значений частоты;
T0 - такт квантования.
Описание:
Процедура возвращает коэффициенты корректирующего звена, реализующего первый закон управления (формула 1.26) по квадратичному критерию (1.24).
Пример:
W := .5*(-93478.39101*z-.1150000000e-3*z^2+902.6600000*z^3
+1026.926837)/(z^5-.5570000000*z^4-124.6542298*z^3
+46.10663267*z^2 +328.8088091*z-4.226757788)
a:=vector(3,[10,100,1000]): Wg:=vector(3,[1,-1,-4]): Т0:=0.063:
sintez2(W, Wg, a, t0);

3 Апробация библиотеки процедур SSO на примере
самолета «Боинг-747»
Для примера взята система стабилизации линейного набора высоты. Уравнения системы имеют вид (1.1), матрицы А и В показаны на (рис. 3.1). Ниже представлено:
1. Нахождение дискретных матриц В (рис.3.1) и А (рис.3.2).
2. Построение особых линий устойчивости по критерию Кларка для дискретных систем (рис.3.2).
3. Нахождение передаточных матриц непрерывной и дискретной систем (рис.3.3).
4. Построение ЛАЧХ и ЛФЧХ непрерывной (рис.3.4) и дискретной (рис.3.5) систем.
5. Построение особых линий устойчивости по критерию Гурвица для непрерывных систем (рис.3.6).
6. Нахождение коэффициентов корректирующего устройства наиболее приближающего желаемую АФЧХ к исходной по двум критериям (рис.3.7).
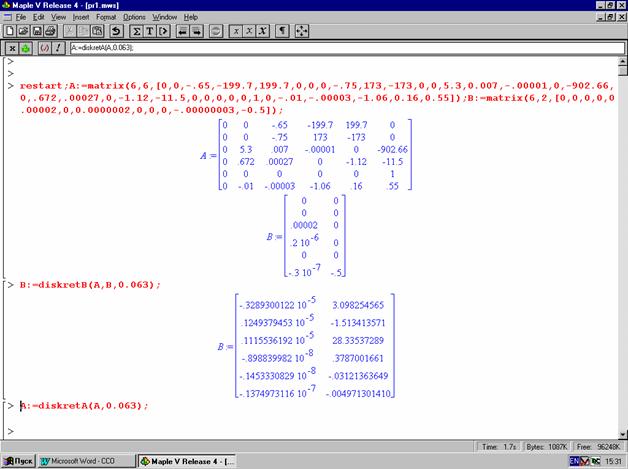
Рис. 3.1
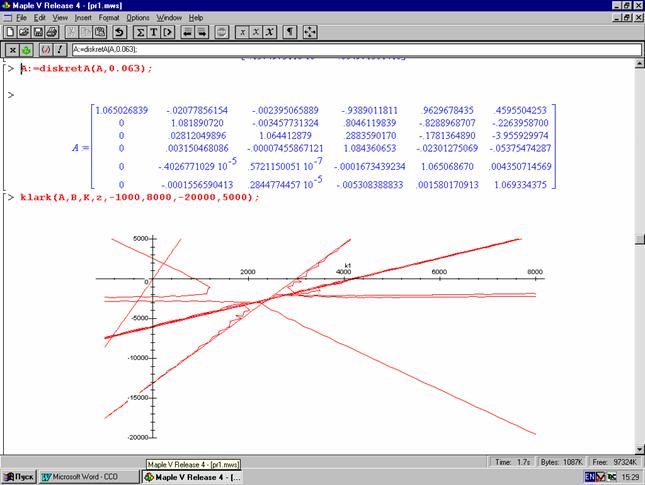
Рис. 3.2
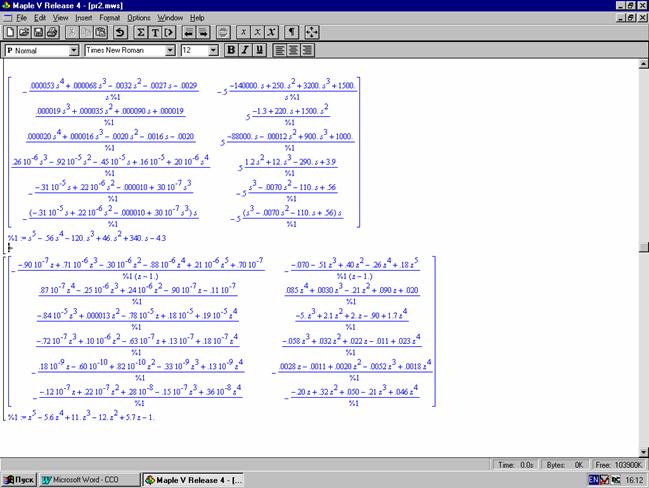
Рис. 3.3
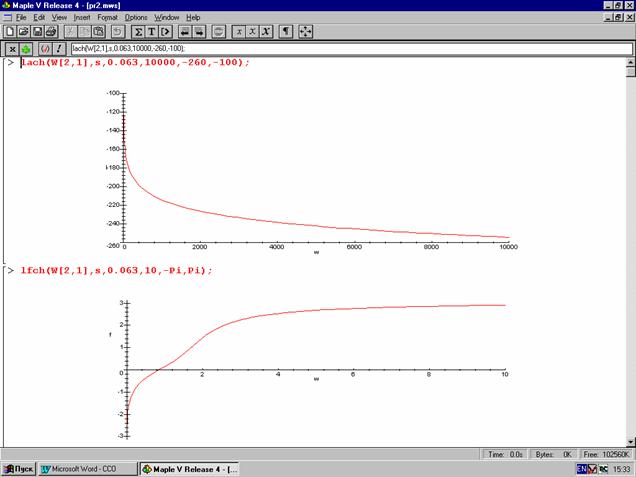
Рис. 3.4
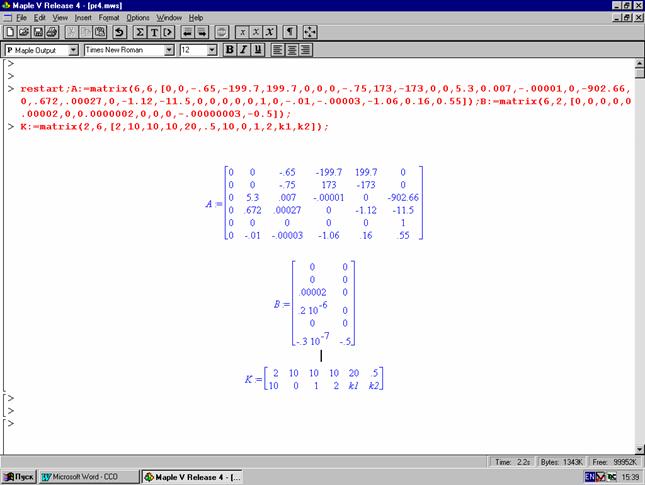
Рис. 3.5
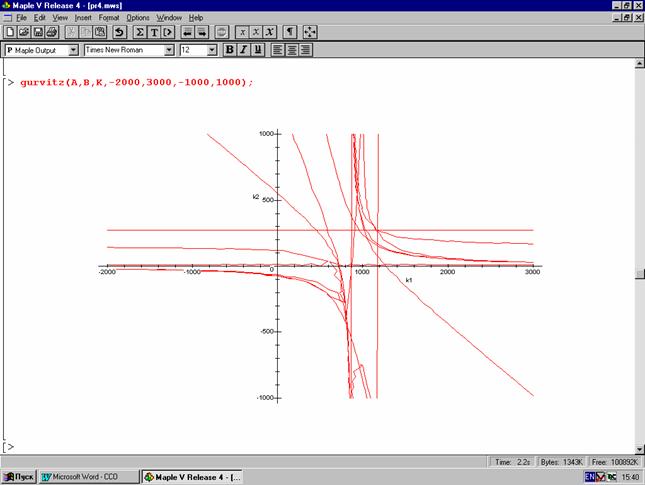
Рис. 3.6
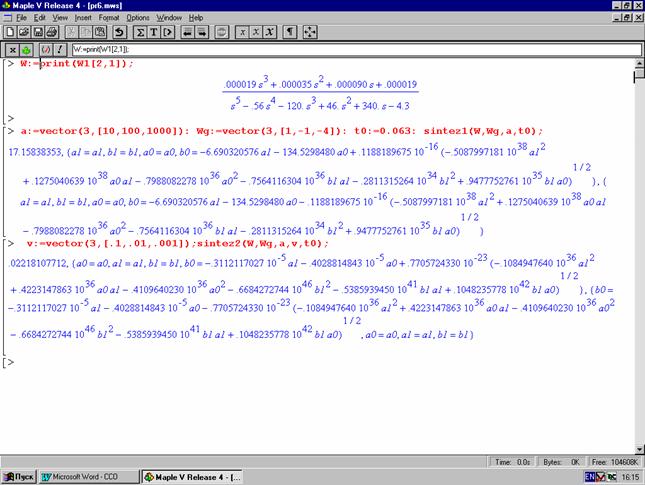
Рис. 3.7
Заключение
1. Решена задача автоматизации анализа и синтеза систем стабилизации с использованием ряда классических методов теории автоматического управления.
2. Разработана библиотека процедур, дополняющая основной математический пакет программ MAPLE V, которая поможет в решении задач анализа и синтеза систем стабилизации и, в частности, в выполнении курсового проекта по дисциплине «Системы стабилизации и ориентации».
3. Библиотека процедур испытана на примере системы стабилизации самолета «Боинг-747», были получены дискретная модель и передаточные функции системы, построены особые линии устойчивости и найдены параметры корректирующего устройства по двум критериям (как видно из результатов второй критерий дает лучшее приближение желаемой характеристики к исходной). Полученные результаты подтверждают высокую эффективность применения результатов работы для автоматизации проектирования систем управления ЛА.
Приложение А
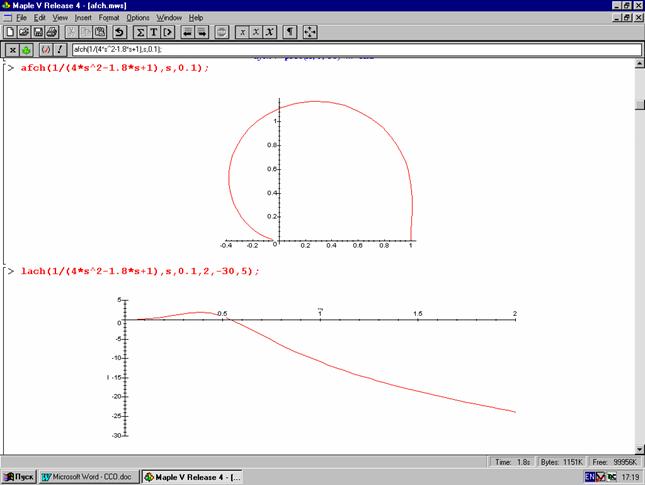
Рис.А.1
Приложение Б
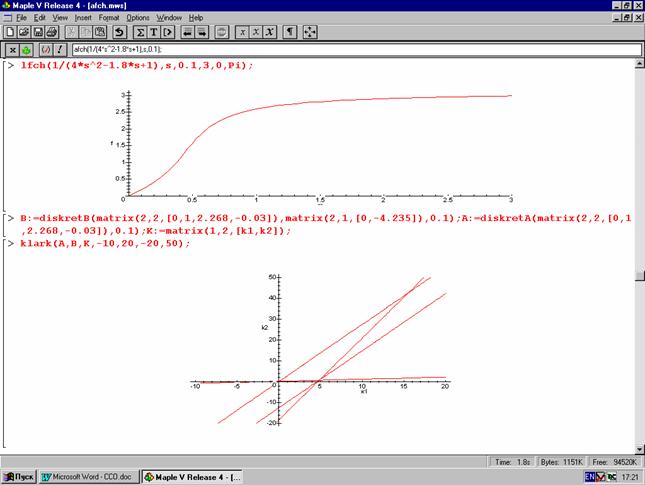
Рис.Б.1
Приложение В
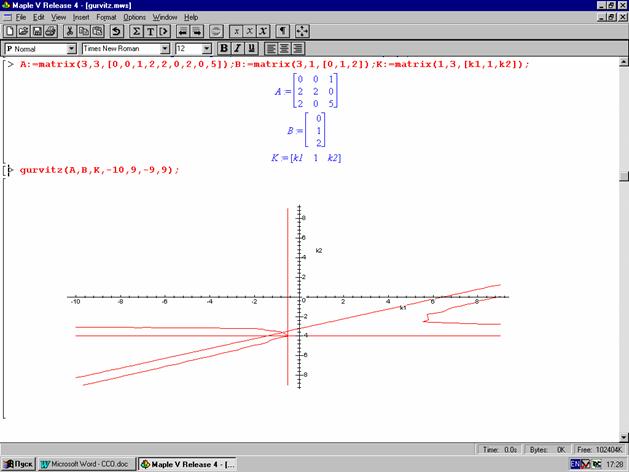
Рис.В.3
Список литературы
1. Айзенберг Я.Е., Сухоребрый В.Г. Проектирование систем стабилизации носителей космических аппаратов.- М.: Машиностроение,1986
2. Бесекерский В.А. Цифровые автоматические системы.- М.: Наука, 1976
3. Борушко Ю.М., Вартанян В.М., Сысун А.И. Системы стабилизации ЛА.- Х.: ХАИ,1989
4. Куо Б. Теория и проектирование цифровых систем управления. - М.:Машиностроение,1986