Полные лекции по аэродинамике и динамике полета
Страница 3
Примерами вихревого движения могут служить:
— плоский сдвиг (когда скорость частиц вдоль некоторой плоскости пропорциональна расстоянию от этой плоскости),
— вращение среды вокруг некоторой оси, как твердого тела (в отличие от потенциального движения аналогичной геометрии в этом случае скорость с удалением от оси линейно возрастает!).
2. ДИНАМИКА СПЛОШНОЙ СРЕДЫ
2.1. Силы и моменты в механике сплошной среды
Силы, распределенные по объему W, называются объемнымиили массовыми. Они обозначаются 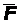 и относятся к элементу массы Dm = rDW. Т.е. сила, действующая на элемент массы, равна
и относятся к элементу массы Dm = rDW. Т.е. сила, действующая на элемент массы, равна 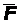 Dm =
Dm = 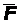 rDW, следовательно, размерность
rDW, следовательно, размерность 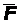 совпадает с размерностью ускорения. Примерами массовых сил могут служить гравитационные, электромагнитные, инерционные.
совпадает с размерностью ускорения. Примерами массовых сил могут служить гравитационные, электромагнитные, инерционные.
Силы, распределенные по поверхности S, называются поверхностными. Поверхностные силы будем обозначать вектором 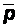 и относить к элементу поверхности DS сплошной среды. Т.е.
и относить к элементу поверхности DS сплошной среды. Т.е. 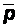 имеет размерность давления. Такие силы возникают, например, на свободной поверхности среды, при взаимодействии среды с твердыми телами, а также внутри среды (внутренние поверхностные силы).
имеет размерность давления. Такие силы возникают, например, на свободной поверхности среды, при взаимодействии среды с твердыми телами, а также внутри среды (внутренние поверхностные силы).
Внутренние поверхностные силы необходимо рассматривать при изучении движения отдельных частиц среды с учетом их механического влияния друг на друга. Так, например, происходит при относительном движении двух соседних соприкасающихся частиц. Это явление может наблюдаться в любом месте сплошной среды, причем для бесконечно малых частиц поверхности соприкосновения dS можно построить любым образом. Тогда и 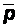 , зависящее от такого выбора, можно определить по-разному в зависимости от dS, т.е. ориентации нормали этой площадки, поэтому такое взаимодействие обозначим вектором
, зависящее от такого выбора, можно определить по-разному в зависимости от dS, т.е. ориентации нормали этой площадки, поэтому такое взаимодействие обозначим вектором 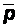 S. В силу третьего закона Ньютона на одну из пары соприкасающихся частиц действует сила
S. В силу третьего закона Ньютона на одну из пары соприкасающихся частиц действует сила 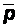 SdS, на другую –
SdS, на другую –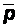 SdS. Однако если соприкосновения нет, т.е. если движение имеет разрыв каких-то своих характеристик, то последнее условие может нарушаться.
SdS. Однако если соприкосновения нет, т.е. если движение имеет разрыв каких-то своих характеристик, то последнее условие может нарушаться.
|

|
 Вектор
Вектор 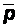 S в общем случае не перпендикулярен к dS, поэтому различают нормальную составляющую pSn, называемую нормальным напряжениемили нормальным давлением, и тангенциальную pSt, называемую касательным напряжениемили внутренним трением:
S в общем случае не перпендикулярен к dS, поэтому различают нормальную составляющую pSn, называемую нормальным напряжениемили нормальным давлением, и тангенциальную pSt, называемую касательным напряжениемили внутренним трением: 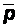 SdS= pSn
SdS= pSn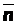 dS + pSttdS.
dS + pSttdS.
Свойство вектора 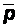 S рассмотрим с помощью представления бесконечно малой частицы в виде тетраэдра с ребрами, параллельными осям координат (рис. 2). Площади граней такого тетраэдра равны S, S×cos(
S рассмотрим с помощью представления бесконечно малой частицы в виде тетраэдра с ребрами, параллельными осям координат (рис. 2). Площади граней такого тетраэдра равны S, S×cos(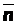 ,x), S×cos(
,x), S×cos(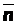 ,y), S×cos(
,y), S×cos(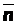 ,z).
,z).
Массовые силы будем считать постоянными во всем объеме W = hS/3 бесконечно малой частицы, а поверхностные силы 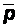 1,
1, 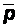 2,
2, 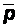 3,
3, 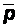 S постоянными на своих гранях. Это позволит применить к частице начало Даламбера из теоретической механики:
S постоянными на своих гранях. Это позволит применить к частице начало Даламбера из теоретической механики:

откуда, сократив на S, и перейдя к пределу при h ® 0, получаем инвариантное к выбору площадки равенство:
 . (2.1)
. (2.1)
Это означает, что существует некоторый объект P, компонентами
которого можно рассматривать векторы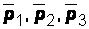 , или даже элементы матрицы (pij) – матрицы из компонент векторов
, или даже элементы матрицы (pij) – матрицы из компонент векторов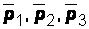 . Объект P с компонентами pij называется тензором внутренних напряжений.
. Объект P с компонентами pij называется тензором внутренних напряжений.
Равенство (2.1) позволяет применить теорему Остроградского-Гаусса (1.10) к расчету поверхностных сил:
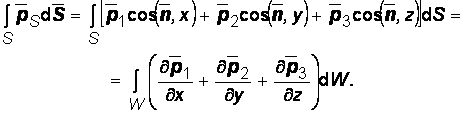 (2.2)
(2.2)
Кроме сил на каждую частицу жидкости могут действовать и моменты. Примером может служить момент магнитного поля Земли, действующий на каждый элемент стрелки компаса. Такой момент, который действует на элемент массы Dm, будем обозначать 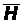 . Его принято называть массовой парой(массовым моментом). Размерность
. Его принято называть массовой парой(массовым моментом). Размерность 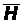 совпадает с размерностью квадрата скорости.
совпадает с размерностью квадрата скорости.
Момент, который действует на элемент поверхности DS, будем обозначать 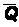 . Он называется поверхностной парой(поверхностным моментом) и имеет размерность силы, деленной на длину.
. Он называется поверхностной парой(поверхностным моментом) и имеет размерность силы, деленной на длину.
2.2. Уравнения движения сплошной среды
В теоретической механике известно уравнение количества движения материальной точки:
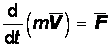 ,
,
где в правой части равенства стоит сумма всех действующих на нее сил. Обобщим это уравнение на конечный объем сплошной среды, состоящей из частиц, как системы материальных точек, подверженных действию рассмотренных в разделе 2.1 объемных и поверхностных сил:
 . (2.3)
. (2.3)
Уравнение количества движения конечного объема сплошной среды(2.3), являющееся аналогом второго закона Ньютона, имеет такое же фундаментальное значение для описания любых движений сплошной среды. Оно справедливо и для разрывных движений, и для ударных процессов, характеризующихся разрывными функциями координат и времени (но не нарушениями гипотезы сплошности – см. раздел 1.1).
Заменив последнее слагаемое в (2.3) с помощью (2.2), получим:
 ,
,
левую часть которого преобразуем с помощью (1.12):
 .
.
Это позволит записать равенство подынтегральных выражений для элементарного объема:
 .
.
Левую часть этого уравнения в свою очередь можно преобразовать с помощью уравнения неразрывности (1.16):

Таким образом, получено основное дифференциальное уравнение движения сплошной среды:
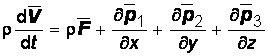 , (2.4)
, (2.4)
или в проекциях на оси декартовой системы координат:
 (2.5)
(2.5)
где  –компоненты массовой силы
–компоненты массовой силы 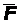 .
.
Отметим, что уравнения (2.4) и (2.5) получены при следующих предположениях:
– непрерывность и дифференцируемость векторов напряжений 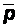 1,
1, 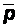 2,
2, 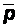 3,
3,