Механико - технологические решения проблемы механизации садо-водства и виноградарства

Страница 8

3.3. Методика нахождения и отображения траектории

сбалансированного роста массива информации

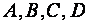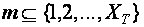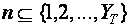Исследованиями установлено, что траекторию сбалансированного роста (ТСР) рационально находить графо - аналитическим методом. Для этого в системе координат по набору издержек в пределах и в масштабе аддитивно отображаются кривые расхода и дохода технологии продукта. На оси абсцисс фиксируется прямая сумма последовательности групп деревьев в периодах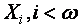

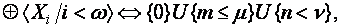(13)

где 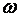- предельно рациональный возраст насаждения;

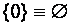- беспериодный (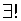) расход времени на закладку насаждения;

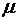- предельное количество «шагов», рекомендуемое на воспитание насаждения, обычно ;

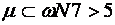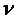- предельно рациональный период эксплуатации насаждения .

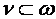На оси ординат аддитивно отображаются: вниз - прямая сумма групп последовательности издержек расхода в периодах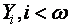

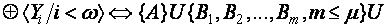
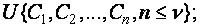(14) вверх - прямая сумма последовательности издержек дохода ;

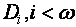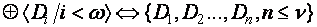. (15)

Тогда разность между выражениями (15) и (14) на фоне последовательности периодов 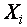(13) даст дискретный массив информации в виде серии последовательных точек в системе координат 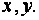В результате каждый информативный момент будет определён двумя противоположно направленными векторными отрезкам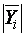и и 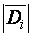. Наложения друг на друга отрезков каждой пары векторов дадут ординаты в виде остатков от разницы отрезков.

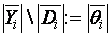
. (16)

Вектор 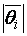своим концом определяет величину баланса пары векторов, а кривая последовательного соединения местоположения балансов всех пар векторов 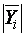и 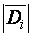будет являть собою ТСР технологического процесса в виде графической модели (рис.8), а с позиции теории логики ТСР может быть квалифицирована, как модель развития технологии, если отобразить её следующей последовательностью:

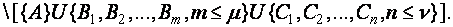(17)

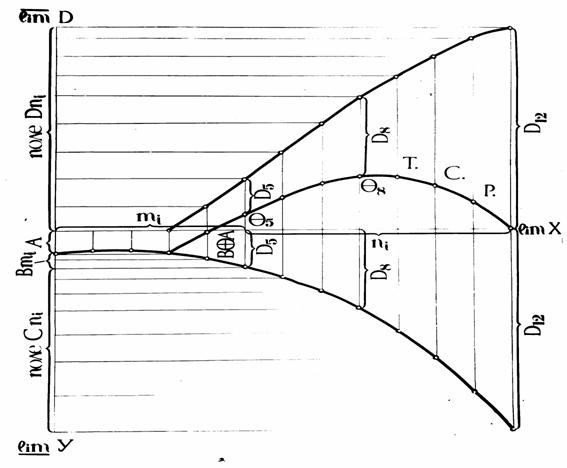
Рис.8. Принципиальное отображение процесса

построения траектории сбалансированного роста

С помощью модели (рис. 8) и последовательности (17), если ТСР отобразить дифференциальным уравнением, может быть определено сравнение технологических процессов в динамике. Возможен вариант построения номограмм на семействе ТСР в зависимости от схем посадок или других параметров насаждений.

3.4. Методика выбора оптимального варианта технологии

Оптимальный вариант выбирается с помощью матричного системного анализа, как наиболее наглядного и легко математизируемого процесса. Для чего, при фиксированном агросроке, тарифные ограничения каждой операции в стадии разносятся по модульной принадлежности в матрицу 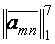, (табл.6), которые чётко рассепарируются на более стабильные информативные поля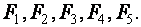

Таблица 6

Матричная модель оптимизации технологи стадии

Модули	Издержки в разрезе модулей	Модели модулей
	ну- ле- вые	почвоуход-ные	удоб-ренче-ские	мелио-ратив-ные	габи-тус-ные	за-щит-ные	убо-роч-ные
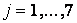
		1	2	3	4	5	6	7
Нулевой	1
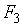
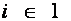
Почво- уходный	2
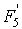
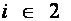
Удобрен-ческий	3
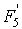
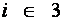
Мелиора-тивный	4
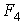
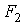
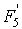
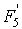
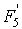
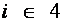
Габи- тусный	5
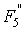
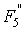
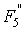
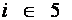
Защит- ный	6
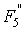
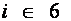
Убороч- ный	7
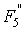
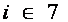