Планета Земля

Планета Земля

Первые астрономические явления, которые с детства знакомы каждому, это — смена дня и ночи, восход и заход Солнца. Объяснение этих явлений связано с вопросом о форме и вращении нашей Земли. На смену наивным представлениям о плоской неподвижной Земле и «небесной тверди» приппо признание шарообразности и вращения Земли и безграничности небес. Доказа­тельства шарообразности Земли черпались из наблюдений формы края земной тени на диске Луны во время лунных затмений, из наблюдений постепенного появления или исчезновения морских судов при их приближении или удалении от берега, из наблюдений изменения высоты Полярной звезды при переезде с севера на юг, из факта расширения горизонта по мере подъема вверх. Идея шарообразности Земли возникла еще у древних греков (Пифагор, VI в. до н. э.: Парменид, VI—V вв. до н. э.; Аристотель, IV в. до п. э.), но потом оставалась в забвении более полутора тысяч лет, до времен Колумба и кругосветных путешествий XVI в.

Размеры земного шара впервые были определены около 240 г. до н. э. Эратосфеном (276—196 гг. до н. э.) в Александрии. Он нашел, что в день летнего солнцестояния в Сиене (южный Египет) Солнце в полдень проходит через зенит, а в Александрии— на расстоянии 1/50 окружности (7°,2) от него. Расстояние между этими городами, расположенными приблизительно на одном меридиане, составляло 5000 греческих стадий. Следовательно, полная окружность равна 250000 стадий, а радиус земного шара R=40 000 стадий. Принимая наиболее вероятную длину стадии равной 160 м, получаем R=6400 км. Современные определения дают R=6370 км.

Вращение земного шара самым естественным образом объясняет смену дня и ночи, восход и заход светил. Широко известны следующие доказательства вращения Земли вокруг своей оси: поворот с течением времени плоскости качаний маятника Фуко относительно окружающих его предметов, сплюснутость Земли, обнаруживаемая из градусных измерений, отклонение падающих тел к востоку, размыв правых берегов рек, текущих в северном полушарии Земли, и левых — в южном полушарии (закон Бэра), пассаты, изменение силы тяжести с широтой (не объясняемое сплюснутостью Земли), направление ветров внутри циклонов и антициклонов и т. д.

Некоторые греческие ученые догадывались и о годичном движении Земли вокруг Солнца. Аристарх Самосский еще в III в. до н. э. считал, что Земля обращается вокруг Солнца. Однако эта идея также оставалась в забвении полторы тысячи лет.Следующие явления можно назвать доказательствами обращения Земли вокруг Солнца: годичный параллакс звезд, годичную аберрацию звезд и смещение линий в спектрах звезд с периодом в один год.

Годичное движение Земли перемещает наблюдателя и этим вызывает видимое смещение более близких звезд относительно более далеких. В течение года близкие звезды описывают на небе (на фоне более далеких звезд) параллактические эллипсы. Большая ось такого эллипса всегда параллельна плоскости земной орбиты, т. е. плоскости эклиптики, а величина оси зависит от расстояния звезды (чем меньше расстояние, тем она больше); величина малой оси зависит, кроме того, и от углового расстояния звезды от плоскости земной орбиты, т. е. от астрономической широты звезды. Годичные параллаксы звезд меньше I". Самая близкая к нам звезда имеет параллакс 0'',76.

Годичное движение Земли вызывает, кроме того, аберрацион­ное смещение звезд; все звезды описывают за год аберрационные эллипсы, большие оси которых всегда равны 41" и параллельные эклиптике, а величины малых осей зависят от астрономической широты звезды. Это аберрационное смещение является результатом сложения скорости движения Земли по ее орбите (в среднем 29,8 км/сек) со скоростью распространения света (около 300000 км/сек), идущего от звезды. В каждый данный момент звезда

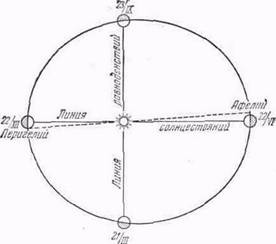
Рис. 1. Земля обращается вокруг Солнца по эллипсу.

смещается в направлении движения Земли, к так называемому апексу орбитального движения Земли. Этот апекс всегда лежит в плоскости земной орбиты под прямым углом к Солнцу на запад от него, т. е. на 90° направо от Солнца.

Годичное движение Земли вызывает также периодическое сме­щение линий в спектрах звезд. Наибольшее смещение линий к крас­ному концу спектра, которое согласно принципу Доплера означает наибольшую скорость удаления от звезды, бы­вает в тот момент, когда геоцентрическая долгота звезды на 90° больше долготы Солнца, наибольшее смещение к фиолетовому концу — при долготе звезды на 90° меньшей долготы Солнца.

Земля движется вокруг Солнца по эллипсу (рис. 1) с эксцентри­ситетом 0,016736 (около 1/60). Солнце находится в одном из фокусов эллипса земной орбиты.Строго говоря, вокруг Солнца движется центр тяжести системы Земля — Луна, так называемый барицентр; вокруг этого центра Земля и Луна описывают в течение месяца свои орбиты. Движение Земли вокруг барицентра с периодом в один месяц вы­зывает периодические колебания в долготах и широтах Солнца и планет. Точное определение амплитуды этих колебаний дает возможность определить расстояние центра Земли от барицентра (барицентр находится на расстоянии 4800 км от центра Земли по направлению к Луне, т. е. на 1600 км под поверх­ностью Земли) и отсюда найти отношение массы Луны к массе Земли.

Среднее расстояние Земли от Солнца равно 149 504 000 км (1 астрономическая единица — а. е.). Эта фундаментальная в астрономии величина выводится из определений солнечного параллакса. Горизонтальным параллаксом Солнца называется угол, под которым на расстоянии Земли от центра Солнца был бы виден экваториальный радиус Земли. Одним из методов измерения солнечного параллакса было наблюдение из разных пунктов на Земле явления прохождения Венеры или Меркурия по диску Солнца.

Самая близкая к Солнцу точка орбиты любой планеты называется перигелием (для Земли это 147 002 000 км), самая далекая— афелием (для Земли 152 006 000 км). Их соединяет линия апсид, совпадающая с большой осью эллипса планетной орбиты. Поло­жение линии апсид определяется гелиоцентрической долготой пе­ригелия. В 1960 г. долгота перигелия земной орбиты близка к 102°. Вследствие медленного вращения линии апсид дол­гота перигелия возрастает на 61",9 в год. В настоящую эпоху Земля проходит через перигелий 2—5 января, а через афелий 1—5 июля. Скорость движения Земли различна в разных частях орбиты. Средняя скорость движения Земли по ее орбите около 30 км/сек или 100 000 км/час; на длину своего поперечника Земля продвигается за семь минут.

Полный оборот вокруг Солнца Земля совершает в течение 365,25636 суток (365d6h9m10s). Это — так называемый звездный, или сидерический, год.

Средний промежуток времени от одного весеннего равно­денствия до следующего, называемый тропическим годом, равен 365,24220 средних суток (365d5h48m46s) *).

Плоскость земного экватора наклонена на 23°27' к плоскости земной орбиты, причем земная ось стремится сохранить неизмен­ным свое направление в пространстве, указывая всегда на северный полюс мира, находящийся вблизи Полярной звезды. Наклон оси вращения Земли и постоянство ее направления являются при­чиной смены времен года на Земле. Продолжительность времен года зависит от эксцентриситета земной орбиты и от расположения линии апсид.

Из градусных измерений было получено, что длина одного градуса широты у экватора равна 110,6 км, а у полюсов —111,7 км. Это приводит к заключению о том, что истинная форма Земли близка к сфероиду. Согласно исследованиям советских геодези­стов (Ф. Н. Красовский и его сотрудники, 1940 г.) экваториальный радиус этого сфероида a=6378,245 км, а полярный b=6356,863 км; разность их a-b=21,382 км.

Сплюснутость земного сфероида характеризуется отношением разности экваториального радиуса а и полярного b к экваториальному. Это отношение очень мало: что составляет около 0,3%, в то время как сплюснутость Юпитера около 6%. Точнейшие геодезические измерения и данные гравиметрии приводят к более точному представлению о фигуре Земли, к понятию о так называемом геоиде. Геоид не является правильной геометрической фигурой; за поверхность геоида принимается некоторая поверхность, в каждой точке перпендикулярная к линии отвеса. Эта поверхность приблизительно совпадает с невозмущенной приливами поверхностью океанов и мысленно продолжается на части Земли, занятые материками. От поверхности геоида отсчитывают высоты различных точек на Земле, когда указывают «высоту над уровнем моря».