Ионно-плазменные двигатели с высоко-частотной безэлектродной ионизацией рабочего тела
Страница 3
1.5 Радиочастотный ионный движитель РИД-26
Этот двигатель интегрирует в себе весь опыт, накопленный в этой области. Радиочастотный безэлектродный разряд и ионно-оптическая система, разработанная для ПИД 10, и нейтрализатор образуют ядро этого двигателя. Потребляя 6 кВт энергии, этот двигатель может развить тягу до 200 мН.
1.6 Радиочастотный двигатель с магнитным полем (РМД)
В последние годы был разработан новый подход к радиочастотным ионным двигателям. Он основан на использовании высокочастотного поля и осесимметричного магнитного поля в разрядной камере для ионизации топлива (рисунок 3). В установке магнитные поля располагаются следующим образом: есть две коллинеарных магнитных катушки, одна из них расположена в задней части разрядной камеры, а другая – на наружной стенке камеры. Рабочее тело поступает в камеры через входное отверстие и газораспределитель, затем с помощью катода-нейтрализатора инициируется разряд. После установления устойчивого разряда в плазме в месте расположения оптимального значения напряженности магнитного поля возникает стоячая волна. В этом случае ток пучка максимален. Двигатель развивает тягу на уровне 1 –10 мН и удельный импульс Iуд=3000 с. Данные, полученные в результате эксперимента, показывают цену тяги около 35 Вт/мН; таким образом этот двигатель относится к той же категории, что и два других ионных двигателя, концепция которых представлена выше. Контроль тяги возможно производить по той же схеме, что и в РИД, а именно посредством измерения ВЧ мощности и расхода рабочего тела. Дополнительно для повышения КПД возможно использовать круговые токи. Эта особенность действительно даст возможность двигателю работать с максимальным КПД даже при очень низких уровнях тяги, что является усовершенствованием по сравнению с предыдущими концепциями.
2 Разработка численной модели электроракетного двигателя с ВЧ нагревом рабочего тела
2.1 Математический аппарат численной модели термогазодинамических процессов, имеющих место в камере и сопловом аппарате ракетного двигателя
Физическая модель процессов, протекающих в электронагревном реактивном двигателе, описывается общей системой уравнений гидрогазовой динамики. Однако на практике наиболее часто используется не она, а набор полуэмпирических формул, полученных на основании обработки большого количества экспериментальных данных, а также некоторые уравнения из общей системы, приведенные к более простому виду благодаря введению ниже перечисленных допущений:
- считается, что скорость рабочего тела, поступающего в камеру РД, равна нулю (wк=0);
- рабочее тело полагается подчиняющимся законам идеального газа, т.е. для него справедливы уравнения состояния идеального газа;
- принимают, что в процессе движения рабочего тела вдоль сопла не происходит теплообмена между рабочим телом и стенками сопла, т.е. процесс истечения адиабатный (Q=0);
- пренебрегают действием внешних сил на поток рабочего тела (Fвн=0);
- пренебрегают вязкостью рабочего тела (ν=0);
- процесс подвода энергии к рабочему телу в камере в высокочастотном разряде считают происходящим в эффективном объеме камеры, составляющем 20% от общего объема камеры.
Приведем основные зависимости параметров рабочего тела в камере РД с учетом вышеизложенных допущений. Скорость истечения газа из реактивного сопла:
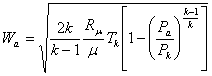 (2.1)
(2.1)
где k – показатель адиабаты рабочего тела;
Rμ=8314 Дж/(кмоль К), универсальная газовая постоянная;
μ – молекулярная масса рабочего тела, кмоль;
Тк - температура в камере сгорания, К;
ра - давление на срезе сопла, Па;
ра – давление в камере,Па.
Площадь среза сопла определяется выражением:
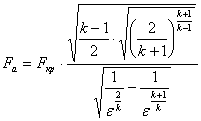
или
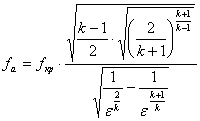 (2.2)
(2.2)
где fкр – удельная площадь критического сечения сопла, м2с/кг;
fа – удельная площадь среза сопла, м2с/кг;
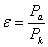 - степень расширения рабочего тела в сопле.
- степень расширения рабочего тела в сопле.
Удельный импульс двигателя:
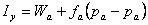 , (2.3)
, (2.3)
где рн – давление окружающей среды, Па;
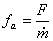 - удельная площадь среза сопла, м2с/кг.
- удельная площадь среза сопла, м2с/кг.
Тяга двигателя определяется по формуле:
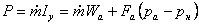 , (2.4)
, (2.4)
где 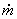 - расход рабочего тела через камеру, кг/с;
- расход рабочего тела через камеру, кг/с;
Fa –площадь среза сопла, м.
Удельная площадь произвольного сечения камеры сгорания и сопла определяется по формуле:
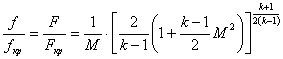 , (2.5)
, (2.5)
где 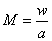 - число Маха в данном сечении сопла;
- число Маха в данном сечении сопла;
w – скорость течения рабочего тела в данном сечении сопла, м/с;
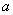 - cкорость звука в данном сечении, м/с.
- cкорость звука в данном сечении, м/с.
Зависимость между степенью расширения рабочего тела в сопле ε и числом Маха на срезе сопла 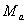 выражается следующей формулой:
выражается следующей формулой:
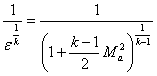 . (2.6)
. (2.6)
Зависимость между поперечными размерами сопла на срезе fa и степенью расширения газа в сопле ε определяется так:
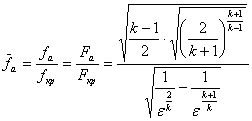 , (2.7)
, (2.7)
Нерасчетный режим работы сопла, когда ра<рн, называется режимом перерасширения и сопровождается проникновением скачков уплотнения внутрь сопла. Начало этого проникновения совпадает с моментом появления скачков уплотнения на срезе сопла, при ра<(0,2 – 0,4)рн. В ходе экспериментов было установлено, что число Маха в сечении, где располагается граница скачков уплотнения при их проникновении внутрь сопла, может быть найдено из уравнения:
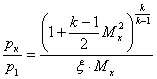 , (2.8)
, (2.8)
где Мх – число Маха в сечении границы скачков уплотнения;
ξ – поправочный коэффициент.
После нахождения из этого уравнения числа Мх можем определить:
- местоположение сечения Х:
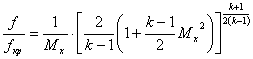 , (2.9)
, (2.9)
- удельный импульс двигателя:
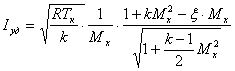 , (2.10)
, (2.10)
- скорость потока рабочего тела в сечение Х:
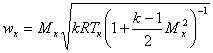 , (2.11)
, (2.11)
- температуру рабочего тела в сечении Х:
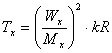 (2.12)
(2.12)
2.2 Термодинамические процессы, протекающие в камере электронагревного движителя
Обобщенно можно представить ТД процессы, протекающие в ЭРД с ВЧ нагревом рабочего тела, следующим образом (см. рисунок 17):
 Рисунок 3. Схема электронагревного ракетного движителя
Рисунок 3. Схема электронагревного ракетного движителя
Запишем уравнение баланса энергии в интегральной форме для промежутка времени 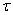 в предположении установившегося процесса работы двигателя:
в предположении установившегося процесса работы двигателя:
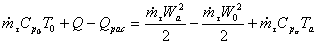 , (2.13)
, (2.13)
где Qрас –потери энергии в двигателе, связанные с рассеянием ее в стенки камеры и сопла и др.;
Ср0, Сра – изобарные теплоемкости рабочего тела соответственно при температурах рабочего тела на входе в камеру и на выходе из сопла, Дж/(кг*К);
Т0, Та - температуры рабочего тела соответственно на входе в камеру и на выходе из сопла, К;
w0, wа – скорости потока рабочего тела соответственно на входе в камеру и на выходе из сопла, м/с.
Разделим все члены записанного уравнения на (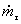
 ), т.е. приведем его к удельной форме:
), т.е. приведем его к удельной форме: