Исследование движения центра масс межпланетных космических аппаратов
Страница 3
Кинематические параметры в геоцентрической экваториальной системе координат:
|
t, сек |
4946.5 |
|
X, м |
6137262,9 |
|
Y, м |
3171846,1 |
|
Z, м |
689506,95 |
|
Vx, м/с |
-201,3 |
|
Vy, м/с |
-1247,03 |
|
Vz, м/с |
7472,65 |
|
l, ° |
28,1 |
Точность выведения:
- предельная ошибка по координате (3s) - 7 км.
- предельная ошибка по скорости (3s) - 5 м/с.
Пересчитав ошибку по координате на ошибку по периоду выведения орбиты получим предельную ошибку по периоду DT - 10 сек.
Корреляционная матрица ошибок выведения на момент выведения составляет:

Члены, стоящие на главной диагонали представляют собой квадраты предельных ошибок - (3s)2.
K11 = K22 = K33 = (3s)2 = 72 = 49 км.
K44 = K55 = K66 = (3s)2 = 52 = 25 м/с.
Остальные члены представляют собой вторые смешанные моменты Kij = Kji = rijsisj или Kij = Kji = rjj(3si)(3sj), где rjj - коэффициенты связи величин i и j. В данном случае вторые смешанные моменты Kij = Kji = 0.
Кинематические параметры в геоцентрической экваториальной системе координат на момент выведения с учетом ошибок выведения:
|
t, сек |
4946.5 |
|
X, м |
6144262,9 |
|
Y, м |
3178846,1 |
|
Z, м |
696506,95 |
|
Vx, м/с |
-206,3 |
|
Vy, м/с |
-1252,03 |
|
Vz, м/с |
7477,65 |
|
l, ° |
28,1 |
Параметры орбиты с учетом ошибок выведения:
|
l, ° |
28,13 |
|
T, c |
5795,7 |
|
W, ° |
28,13 |
|
p, км |
6973,5 |
|
а, км |
6973,6 |
|
e |
0,00314 |
|
i, ° |
97,637 |
2.3.2. ЦЕЛИ РАБОТЫ
1) Исследование и моделирование движения ЦМ МКА при воздействии на КА возмущающих ускорений.
2) Разработка алгоритмов проведения коррекции траектории МКА, моделирования процесса, и расчет потребного топлива для проведения коррекции траектории.
3) Исследование динамики системы коррекции траектории при стабилизации углового положения в процессе проведения коррекции траектории МКА.
2.4. МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС МКА
2.4.1.УРАВНЕНИЕ ДВИЖЕНИЯ КА
Рассмотрим невозмущенное движение материальных точек М и m в некоторой инерциальной системе координат. Движение совершается под действием силы притяжения Fz. Сила Fz для материальной точки m определяется формулой:
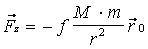 ,
,
где ¦ - постоянная притяжения,
ro - единичный вектор, направленный от М к m,
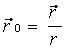 ,
,
где 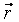 - радиус-вектор, проведенный из т.М до т.m.
- радиус-вектор, проведенный из т.М до т.m.
r - относительное расстояние от М до m.
На точку М действует сила Fz, равная по величине и направленная в противоположную сторону.
На основе второго закона Ньютона уравнения движения материальных точек М и m имеют вид:
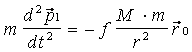 (1),
(1), 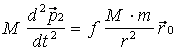 (2)
(2)
или
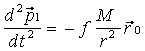 (3),
(3), 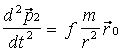 (4)
(4)
где p1 - радиус-вектор, проведенный из начала инерциальной системы координат в точку m.
p2 - радиус-вектор, проведенный из начала инерциальной системы координат в точку М.
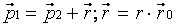 .
.
Вычитая из уравнения (3) уравнение (4), получим уравнение движения материальной точки m относительно притягивающего центра М:
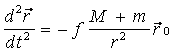

Так как m<<М, следовательно, можно пренебречь ускорением, которое КА с массой m сообщает притягивающему центру М. Тогда можно совместить начало инерциальной системы координат с притягивающим центром М. Следовательно, 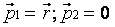 .
.
Таким образом, уравнение невозмущенного движения КА относительно притягивающего центра М в инерциальной системе координат, центр которой находится в М, имеет вид
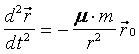 ,
,
где m = fM - гравитационная постоянная Земли.
Рассмотрим возмущенное движение КА в геоцентрической экваториальной (абсолютной) системе координат OXYZ:
- начало О - в центре масс Земли.
- ось X направлена в точку весеннего равноденствия g.
- ось Z совпадает с осью вращения Земли и направлена на Северный полюс Земли.
- ось Y дополняет систему до правой.
Движение КА в абсолютной системе координат OXYZ происходит под действием центральной силы притяжения Земли Fz, а также под действием возмущающих сил Fв. Уравнение движения имеет вид
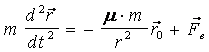 или
или 
где m = 597 кг - масса КА.
В проекциях на оси абсолютной системы координат OXYZ получим
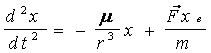 или
или 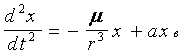
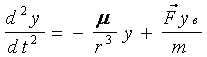 или
или 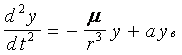
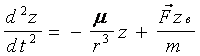 или
или 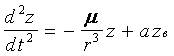
где axв, ayв, azв - возмущающиеся ускорения.
Основные возмущающиеся ускорения вызываются следующими причинами:
- нецентральностью поля притяжения Земли.
- сопротивлением атмосферы Земли.
- влиянием Солнца.
- влиянием Луны.
- давлением солнечного света.