Расчет средней доходности, прогнозирование затрат на привлеченные и размещенные средства, моделирование оптимального привлечения и размещения средств

Страница 3

a - рост затрат

x - объем привлеченных (размещенных) средств

Подставив имеем следующую формулу:

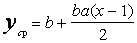, тогда (6)

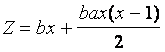(7)

Теперь можно рассчитать доход от привлечения (размещения) x объема средств.

D1=xS-Z, где (8)

S - разница между доходностью активных операций и ставкой по привлеченным средствам

D1 - доход от привлечения x единиц денежных средств, за вычетом расходов.

Подставив формулу 7 получаем:

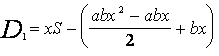(9)

тогда первая производная по x:

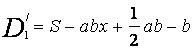(10)

Приравняем D|1=0, и найдем объем привлеченных средств, при котором D максимально:

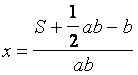(11)

Остается подставить в формулу значения затрат, роста затрат и разницу между доходностью и ставкой по привлеченным ресурсам и можно найти x, при котором доход финансового субъекта будет максимален, и к которому необходимо стремиться. Однако данные формулы учитывают только затраты на привлечение средств, но существуют также затраты на размещение средств, предположим, что они тоже распределяются линейно, но имеют другие значения a и b, роста и затрат на первую единицу соответственно. Тогда:

D2 = xS-Z1-Z2, где (12)

Z1 - затраты на привлечение средств

Z2 - затраты на размещение средств

Подставив 7 получаем:

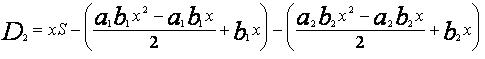, где (13)

b1 - затраты на первую единицу привлеченных средств

a1 - рост затрат привлечения средств

b2 - затраты на первую единицу распределенных средств

a2 - рост затрат распределения средств

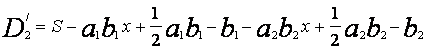(14)

Если D|2=0 получаем:

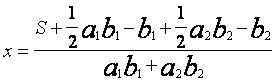(15)

По формуле 15 можно вычислить оптимальное значение x, по формуле 13 можно найти максимальное значение дохода при объеме привлеченных средств x.

Таким образом формулы 12-15 отражают адекватную модель финансового субъекта, имеющего один вид привлеченных ресурсов и один вид распределенных средств, если затраты на привлечение и размещение средств изменяются линейно.

Рассмотрим оптимальное распределение размещенных средств между двумя проектами, при наличии у кредитного учреждения суммы x, предполагая что она полностью может быть использована на каждый проект в отдельности.

D3 = LP1+(x-L)P2-Z1-Z2, где (16)

D3 - доход от кредитования

P1 - доходность 1 проекта (для удобства расчетов проект с большей доходностью)

P2 - доходность 2 проекта

L - сумма на 1 проект

(x-L) - сумма на 2 проект

Z1 - затраты на 1 проект при сумме L

Z2 - затраты на 2 проект при сумме (x-L)

Подставим в формулу 16 значения Z1 и Z2:

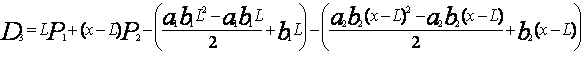(17)

Преобразовав получаем:

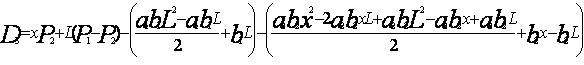(18)

Тогда первая производная по L формулы 18:

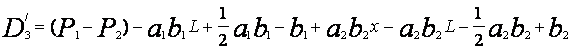(19)

Если D|3=0 получаем:

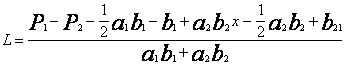(20)

По формуле 20 можно рассчитать оптимальное значение L - средства на 1 проект, средства на 2 проект соответственно равны - (x-L). При таком распределении средств между проектами доход будет максимальным. Аналогично можно рассчитать распределение сумм средств между источниками привлекаемых средств если известна необходимая для размещения сумма.

Финансовые институты, занимающиеся перераспределением средств, т.е. совмещающие привлечение и распределение средств для расчета оптимального объема ресурсов могут использовать формулы 13, 15, в которых смоделирован процесс перераспределения средств для структуры с одним источником привлеченных средств (например: вклады населения) и одним видом клиентов по размещению ссуд (например: физические лица).

Другие субъекты финансового рынка , решающие задачи по распределению средств между 2 проектами (привлечения или размещения не имеет значения) если известна сумма средств, могут использовать формулы 18,20 в которых смоделирован процесс привлечения (размещения) средств из 2 источников. Данные формулы дают возможность определить точку максимального дохода от вложения средств в разные проекты.

Также имеющиеся модели можно использовать для решения задачи привлекательности инвестиций с учетом ликвидности, если затраты на инвестирование примерно равны в обоих вариантах, но существуют вопросы по оптимальному соотношению ликвидность/рентабельность, то получив методом экспертных оценок зависимость уменьшения (увеличения) ликвидности от объема предоставленного кредита в тот или иной проект можно просчитать оптимальное соотношение, подставив вместо изменения затрат изменение ликвидности.