Межбанковский клиринг

Страница 7

2. Чем меньше лаг клиринга, тем больше требуется ликвидных средств для проведения совокупных расчетов. Значит, имеем отвлечение средств и, следовательно, име­ем потенциальные потери банка-плательщика. Ясно, что при стремлении лага к нулю отвлечение достигает како­го-то максимума V, а при стремлении лага к бесконечно­сти отвлечение достигает какого-то минимума I.

Итак, происходит конкуренция двух факторов:

1) потенциальная потеря от замораживания средств в клиринге, которая пропорци­ональна времени замораживания и

2) потенциальный доход от уменьшения средств обеспечения расчетов, ко­торое растет с ростом лага клиринга.

Интегральный эф­фект клиринга есть разность этих двух величин. Значит, и слишком малый лаг клиринга плох, и слишком большой лаг клиринга плох. Следовательно, есть оптимальный лаг и его нужно определить.

Задача состоит в том, чтобы определить лаг клирингового цикла, при котором интегральный эффект клиринга будет максимальным.

2.2. Формализация задачи

Формула расчета убытка от применения клиринга вследствие простаивания денег клирингового пакета имеет следующий вид:

,

где – интенсивность оборота, сколь­ко средств проходит в валовых расчетах за единицу вре­мени – за день. Эта формула показывает отвлечение вследствие клиринговой неподвижности средств платежного пакета, как следствие клиринга Средства были бы пущены в оборот и принесли бы выгоду банкам-получателям средств. Итак, имеем здесь дело с потенциальным убытком. Предполагая равномерное поступление платежей, имеем простой средств в размере в течение времени , т.е. .

Теперь подсчитаем доход: на оплату требуется меньше средств, чем при валовой оплате, а сэкономленные средства пускаются в оборот и приносят доход.

Таким образом имеется возможность построить математическую модель:

Пусть, - средства, необходимые для поддер­жания клиринга, – лаг клиринга. Накладываются следующие естественные условия:

1) При (2.1),

где – средства, обслуживающие валовые расчеты.

2) При (2.2),

где – средства, обслуживающие «экспорт-импорт» кли­ринговой системы;

3) есть функция от .

Найдем вид функции , основываясь, как говорят в физике, на феноменологическом подходе. Т.е. мы не привлекаем никаких «микродеталей» типа статисти­ки потоков между участниками и т.д., а основываемся только на самых общих «внешних» соображениях. Внут­ренний причинный механизм денежных потоков остается черным ящиком. Воспользуемся однородностью времени. Все возможные лаги клиринга обра­зуют ось – ось лага клиринга. Очевидно, что ни один момент времени не должен быть выделен: если у нас был лаг клиринга и мы переходим к , то все равно, как мы считаем – или отталкиваясь от 0, беря за основу , или отталкиваясь от , беря за основу . Графическая интерпретация изложенного дана на Рис. 3.1.

Итак, однородно и, значит, имеем своего рода прин­цип относительности: закон не должен зависеть от си­стемы координат. В применении к нашему случаю это означает, что формула О должна давать ковариантную (не изменяющую вида) зависимость от : сдвиг по оси не должен менять вида формулы, если пересчитать все к новому началу координат – переход от к = - а и от к должен удовлетворять условию . Или, по другому, . Такое функциональное уравнение характерно только для экспоненты.

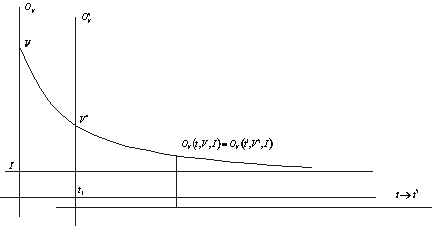Рис.2.1. Графическая интерпретация «однородности» времени.

В дифференциальном виде экспонента характеризуется соотношением:

(2.3),

где v – какой-то коэффициент пропорциональности. Условия (1) - (3) дают единственное решение:

(2.4)

Проверяем выполнение свойства :

, что и нужно.

Данная математическая модель подсчета средств, необходимых для поддержания клиринга, была разработана и протестирована на адекватность и устойчивость в американской клиринговой системе CHIPS, кроме того, адекватность данной модели подтверждена проверкой на отечественных статистических данных по межбанковским расчетам в информационно-аналитическом управлении Белорусского Межбанковского Расчетного Центра Национального Банка Республики Беларусь.

Используя этот результат, подсчитаем экономию вследствие клиринговости.

Итак, – реальное отвлечение вследствие «валовости» (об этом говорит ин­декс параметра О), т. е. расчетов через конечный отрезок времени , а не бесконечный, что было бы идеальным для клиринга. Параметр – это максимум средств, для под­держки расчетов, достигаемый при чистом вале, когда клиринга нет: . Параметр – это минимум средств для поддержки расчетов, достигаемый при чистом клиринге, когда валовой оплаты нет: . Параметр – это мера спада потребности в средствах для расчетов. Его можно определить эмпирически по результатам кли­ринга с циклом в один день. Пусть, в этом случае, требу­ются для обеспечения расчетов средства в размере . Тогда

(2.5)